
ॐ जितेन्द्र सिंह तोमर
(M.A., B. Ed., MASSCOM, DNYS )
(Specialist in Basic and Vedic Maths)
यह बिल्कुल नया टॉपिक है इसलिए इसे एक बार पुनः रिवाइज कर लेते हैं । हम तीसरे अध्याय में भी विनकुलम के बारे में पढ़ चुके हैं। आईए एक बार फिर से रिवीजन कर लेते हैं।
विनकुलम अंक
* रेखांक या रेखांकित अंक या ऋणात्मक अंक या विनकुलम अंक
* सामान्य संख्याओं को विनकुलम बनाना
* विनकुलम संख्याओं को सामान्य संख्या बनाना
Vinjit Vedic Arithmetic Book || 1 || Chapter 03.02 || Rekhaank or Rekhaankit ank or Negative digit or Vinculum ank
This is a completely new topic so let's revise it once again. We have also read about vinculum in the third chapter. Let's revise it once again.
* Rekhaank or Rekhaankit ank or Negative digit or Vinculum ank
* Converting normal numbers into vinculum and Converse
* Normalizing Vinculum numbers
Author

ॐ जितेन्द्र सिंह तोमर
(M.A., B. Ed., MASSCOM, DNYS )
(Specialist in Basic and Vedic Maths)
(1) साधारण एवं वैदिक संख्याएं :
गणित की साधारण प्रणाली में हम जिन संख्याओं का प्रयोग करते हैं उनके सभी अंक धनात्मक होते हैं। उदाहरणार्थ: संख्या 123546 के सभी अंक 1, 2, 3, 5, 4 और 6 धनात्मक हैं।
परन्तु वैदिक गणित में ऐसी संख्याओं का भी प्रयोग किया जाता है जिनके सभी अंक या तो धनात्मक हों या ऋणात्मक हों या फिर दोनों ही प्रकार के अर्थात अंक धनात्मक तथा ऋणात्मक दोनों ही प्रकार के हो सकते हैं।
अब प्रश्न उठता है कि वैदिक गणित में ऋणात्मक अंकों का प्रयोग क्यों और किस प्रकार से होता है?
इस प्रश्न का उत्तर है कि वैदिक गणित में प्रयुक्त संख्याओं के सभी अंक 5 अथवा 5 से छोटे रखे जाते हैं। वैदिक गणित में बड़े अंकों 6, 7, 8, 9 का प्रयोग नहीं किया जाता है। तो आपके दिमाग में एक प्रश्न आता होगा कि वैदिक गणित इन अंको की कमी कैसे पूरी करता है?
वैदिक गणित पांच से बड़े अंकों 6, 7, 8, 9 को छोटे अंकों में परिवर्तित कर लेते हैं। पांच से बड़े अंकों 6, 7, 8, 9 को छोटे अंकों में परिवर्तित करने की प्रक्रिया में ऋणात्मक अंक प्राप्त होते हैं। इन ऋणात्मक अंकों को विनकुलम् अंक कहते हैं ।
अतः वैदिक संख्या में धनात्मक तथा ऋणात्मक दोनों ही प्रकार के अंकों का समावेश हो जाता है।
(1) Ordinary and Vedic numbers:
Generally, all the digits of the numbers we use in mathematics are positive. For example: All the digits 1, 2, 3, 5, 4 and 6 of the number 123546 are positive.
But in Vedic mathematics such numbers are also used whose all digits are either positive or negative or can be of both types i.e. both positive and negative.
Now the question arises that why and how are negative numbers used in Vedic mathematics?
The answer to this question is that all the digits of the numbers used in Vedic mathematics are kept 5 or smaller than 5. Big numbers 6, 7, 8, 9 are not used in Vedic mathematics. So a question might come to your mind that how does Vedic Mathematics fulfill the shortage of these numbers?
In Vedic Mathematics digits greater than five, 6, 7, 8, 9 are converted into smaller digits. In the process of converting numbers larger than five, 6, 7, 8, 9 into smaller numbers, negative numbers are obtained. These negative numbers are called Vinkulam numbers.
Therefore, Vedic numbers include both positive and negative numbers.
1. सामान्य अंक
यदि अंकों का उपयोग हम सामान्यतः गणितीय अंकों के रूप में करते हैं। तो यही अंक सामान्य अंक कहलाते हैं। अतः सामान्यतः गणित में ये दस अंक 0, 1, 2, 3, 4, 5 6, 7, 8, 9 हैं। इनका उपयोग हम सामान्यतः गणित में करते हैं।
1. Normal Digits
If we use diits in the form of mathematical digits, then these digits are called common digits. So, in general ten digits, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. are generally use them in mathematics.
2. वैदिक अंक
वैदिक गणित में केवल 14 प्रकार के अंको का ही उपयोग किया जाता है। जो निम्न हैं → 0, 1, 2, 3, 4, 5, 6 या –4, 7 या –3 , 8 या –2, 9 या –1 आदि।
अतः वैदिक गणित में ये चौदह अंक 0, 1, 2, 3, 4, 5 6, 7, 8, 9, –1, –2, –3, –4 हैं। इनका उपयोग हम वैदिक गणित में करते हैं।
2. Vedic Digits
Only 14 types of digits are used in Vedic mathematics. Which are as follows –> 0, 1, 2, 3, 4, 5, 6 or –4, 7 or –3, 8 or –2, 9 or –1 etc.
Hence, in Vedic mathematics these fourteen digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, –1, –2, –3, –4. We use these in Vedic mathematics.
विनकुलम्
जैसा कि हम आपके विनकुलम अंको के बारे में जानकारी दे चुके हैं आईए अब विस्तार से उनके बारे में जानते हैं।
वैदिक गणित ( Vedic Mathematics ) में संख्याओं में अंकों को ऋणात्मक रूप में लिखने को विनकुलम् कहते हैं और इन अंकों को विनकुलम् अंक कहते हैं।
वैदिक गणित में ऋणात्मक अंक ( –m ) को, अंक m के ऊपर ऋणात्मक (बार /रेखा) या m के ऊपर डेश चिह्न द्वारा व्यक्त किया जाता है।
अतः वैदिक गणित में ऋणात्मक अंक (–4) को, अंक 4 के ऊपर ऋणात्मक चिन्ह या डेश लगाकर 4' व्यक्त किया जाता है जो (–4) का विनकुलम् 4' अथवा बिनकुलम् कहलाता है।
Vinkulam
As we have already given you information about your Vinkulam digits, let us now know about them in detail.
In Vedic mathematics, the writing of digits in negative form is called Vinkulam and these digits are called Vinkulam Digits.
In Vedic mathematics, a negative digit (–m) is expressed by putting a negative sign (bar / Line) or dash above the digit m or by a (bar / Line) or dash symbol.
Therefore, in Vedic mathematics, the negative number (–4) is expressed as 4' by putting a negative sign or dash above the number 4, which is called Vinakulam 4' or Binakulam of (–4).
विनकुलम् का सिद्धान्त :
पांच से बड़े अंकों 6, 7, 8, 9 को छोटे अंकों में परिवर्तित करने की प्रक्रिया को विनकुलम् कहते हैं । जिससे इनके छोटे व ऋणात्मक अंक प्राप्त होते हैं । इन छोटे व ऋणात्मक अंकों को विनकुलम् अंक कहते हैं ।
जैसा कि हम पहले ही बता चुके हैं कि वैदिक गणित में प्रयुक्त होने वाली संख्याओं में सभी अंक 5 अथवा 5 से छोटे रखे जाते हैं। अतः संख्या मैं जो भी अंक 5 से बड़े (6, 7, 8, 9) होते हैं, उन सभी अंकों के स्थान पर उनके विनकुलम् अंक रख कर उपयुक्त क्रिया करते हैं।
Principle of Vinkulam:
The process of converting numbers 6, 7, 8, 9 larger than five into smaller numbers is called Vinkulam. Due to which they get small and negative marks. These small and negative numbers are called Vinkulam numbers.
As we have already told that in the numbers used in Vedic mathematics, all the digits are kept 5 or smaller than 5. Therefore, all the digits in the number which are greater than 5 (6, 7, 8, 9) are replaced by their Vinkulam digits and appropriate actions are performed.
विनकुलम् अंकों के अन्य नाम
विनुकुलम अंको को हम रेखांक या रेखांकित अंक या ऋणांक या ऋणात्मक अंक या विनकुलम या डेश डिजिट या बार डिजिट आदि के नाम से भी जानते हैं।
Other names of Vinkulam digits
We also know Vinukulam digits by the name of lineer digits (rekhaank ) or underlined digit (rekhaankit ank ) or negative digit or negative digit (rinaank ) or Vinkulam or dash digit or bar digit etc.
रेखांक, रेखांकित अंक, ऋणांक या ऋणात्मक अंक या विनकुलम
रेखांक– रेखांक एक ॠणात्मक अंक होता हैं, जिसे उसके ऊपर रेखा खींच कर व्यक्त करते हैं।
Rekhaank or Rekhaankit ank or Negative digit or Vinculum ank
Rekhank :–Rekhank is a negative number or a digit with a bar on its top, this bae is used to show a negative number.
वैदिक गणित को सीखने के लिए विनकुलम् के सिद्धांतों को जानना बहुत ही आवश्यक है। विनकुलम् को वैदिक गणित में रेखांक या रेखांकित अंक या ऋणांक या ऋणात्मक अंक के नाम से भी जाना जाता है।
वर्तमान में गणित में संकलन, व्यवकलन, गुणा और भाग में एक ही समय में केवल दस धनात्मक संख्याओं (शून्य से नौ तक 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ) का प्रयोग किया जाता है अर्थात उसके सभी अंक धनात्मक होते हैं।
इस प्रकार हम कह सकते हैं कि वैदिक गणित में हम निम्न चौदह अंकों का ही उपयोग करते हैं जैसे 0, 1, 2, 3, 4, 5, 6 या –4 या 4', 7 या –3 या 3' , 8 या –2 या 2', 9 या –1 या 1' आदि।
जैसे –* एक अंक की संख्या 7 अंक धनात्मक हैं।
* दो अंक की संख्या 75 के सभी अंक धनात्मक हैं।
* तीन अंक की संख्या 785 के सभी अंक धनात्मक हैं।
इसी प्रकार बड़ी संख्या संख्य 8273505 के सभी अंक धनात्मक हैं।
Rekhaank or Rekhaankit ank or Vinkulam – Theory and Application
It is very important to know the principles of Vinkulam in order to learn Vedic Mathematics. Vinkulam is also known as Rekhaank or Rekhaankit ank or Negative Number or dash digit in Vedic mathematics.
At present, only ten positive numbers (Zero to nine 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ) are used in addition, subtraction, multiplication and division in mathematics. That is, all numbers are positive in mathematics.
Thus we can say that in Vedic maths we use only 14 following numbers like 0, 1, 2, 3, 4, 5, 6 or –4 or 4' , 7 or –3 or 3' , 8 or –2 or 2', 9 or – 1 or 1' etc.
For Example
* All the digits of the single digit number 1, 3, 7, 6, 5 are positive.
* All the digits of the two digit number 75 are positive.
* All the digits of the three digit number 785 are positive.
Similarly all the digits of the big number number 8273505 are positive.
वैसे तो वैदिक गणित में 0 से 9 तक सभी अंकों का उपयोग होता है, परंतु अपनी सुविधा और कुछ गणनाओं को सुलभ बनाने के लिए हम इन्हें 5 या 5 से छोटे अंक या संख्याओं के रूप में ही लेते हैं। अर्थात इन गणनाओं में बड़े अंकों 6, 7, 8, 9 का प्रयोग नहीं किया जाता है।
अंक 6, 7, 8, 9 को छोटे अंकों में परिवर्तित करने की प्रक्रिया में हमें ऋणात्मक अंक प्राप्त होते हैं। साथ ही वैदिक गणित में धनात्मक एवं ऋणात्मक दोनों प्रकार के अंकों का प्रयोग किया जाता है।
Although all the numbers from 0 to 9 are used in Vedic mathematics, but for our convenience and to make some calculations accessible, we take them as numbers or numbers less than 5 or 5 only. That is, the big numbers 6, 7, 8, 9 are not used in these calculations.
In the process of converting the numbers 6, 7, 8, 9 into smaller numbers, we get negative numbers. Also, both positive and negative numbers are used in Vedic mathematics.
वैदिक गणित में प्रयुक्त होने वाली संख्याओं के सभी अंक 5 या 5 से छोटे रखे जाते हैं।
वैदिक गणित ( Vedic Mathematics ) में संख्याओं के अंकों को ऋणात्मक रूप में लिखने को विनकुलम् कहते हैं। वैदिक गणित में ऋणात्मक अंक ( –2 ) को, अंक 2 के ऊपर ऋणात्मक चिह्न लगाकर याा बार चिन्ह द्वारा व्यक्त किया जाता है। हम यहां इसे –2 या 2' लिखेंगे। जो विनकुलम् दो या ऋण 2 पढ़ा जाएगा।
वैदिक गणित में प्रयुक्त होने वाली संख्याओं में सभी अंक 5 या 5 से छोटे रखे जाते हैं। अतः संख्या में जो भी अंक 5 से बड़े ( 6, 7, 8, 9 ) होते हैं, उन सभी ( 6, 7, 8, 9 ) अंकों के स्थान पर उनके विनकुलम् अंक रख देते हैं।
All digits of numbers used in Vedic maths are kept as 5 or less than 5.
In Vedic Mathematics, writing the digits of numbers in negative form is called Vinkulam. In Vedic mathematics, a negative number (–2) is expressed by putting a negative sign above the number 2 or by a bar symbol. Here we will write it as –2 or 2'. Which will be read Vinkulam two or minus 2.
In the numbers used in Vedic mathematics, all numbers are kept 5 or less than 5. Therefore, whatever digits are greater than 5 (6, 7, 8, 9) in the number, all those (6, 7, 8, 9) digits are replaced by their Vinkulam digits.
इस प्रकार हम कह सकते हैं कि वैदिक गणित में हम गणना को छोटा वह सरल बनाने के लिए शून्य सहित प्राकृतिक अंकों के साथ साथ विनकुलम अंकों का उपयोग करते हैं । इस प्रकार वैदिक गणित में केवल 14 प्रकार के अंकों का ही उपयोग किया जाता है। जो निम्न हैं → 0, 1, 2, 3, 4, 5, 6 या –4, 7 या –3 , 8 या –2, 9 या –1 आदि।
Thus we can say that we use vinculum numbers along with natural numbers including zero to make calculations small and simple in Vedic Maths. Thus only 14 types of digits are used in Vedic mathematics. Which are as follows → 0, 1, 2, 3, 4, 5, 6 or –4, 7 or –3, 8 or –2, 9 or –1 etc.

किसी अंक का विनकुलम् अंक या विनकुलम् ज्ञात करना :
5 से बड़े जिस अंक का भी विनकुलम् ज्ञात करना होता है। विनकुलम् बड़े अंक का '10 से ऋणात्मक विचलन' होता हैं।
चूंकि 5 से बड़े अंक 6, 7, 8 और 9 सभी 10 से कम हैं, इसलिए इनके 10 से विचलन ऋणात्मक चिन्ह वाले होंगे। विचलन से प्राप्त इन अंकों को उनके सामने ऋणात्मक चिन्ह (–) या ऊपर डेश चिन्ह ( ' ) लगाकर प्रदर्शित किया जाता है। इन रेखांकित अंकों को विनकुलम् या विनकुलम् अंक कहते हैं।
उदाहरणार्थ
अंक 6 का विनकुलम् ज्ञात करना।
अंक 6 का 10 से विचलन = 6 –10 = –4 या 4'
अंक 6 का विनकुलम् (अंक) = –4 या 4'
इसी प्रकार, अंक 7 का विनकुलम् (अंक) = 7–10=–3 या 3'
तथा
अंक 8 को विनकूलम् (अंक) = 8–10=–2 या 2'
अंक 9 का विलकुलम् (अंक) =9–10=–1 या 1'
To find Vinkulam number or Vinkulam of a number:
Vinkulam of any number greater than 5 has to be found. Vinkulam is the 'negative deviation from 10' of the larger number.
Since numbers greater than 5, 6, 7, 8 and 9 are all less than 10, their deviations from 10 will have negative signs. These numbers obtained from deviations are displayed by putting a negative sign (–) in front of them or a dash sign (') above them. These underlined numbers are called Vinkulam or Vinkulam numbers.
For Example
To find Vinkulam of number 6.
Deviation of number 6 from 10 = 6 –10 = –4 or 4'
Vinkulam (digit) of number 6 = –4 or 4'
Similarly, Vinkulam (digit) of number 7 = 7–10=–3 or 3'
And
Vinkulam (digit) of number 8 = 8–10=–2 or 2'
Vilakulam (digit) of number 9 =9–10=–1 or 1'
(6) निखिलम् सूत्र :
निखिलम् सूत्र है –
'निखिलम् नवत: चरमं दशतः' अर्थात 'प्रत्येक अंक को 9 में से तथा अन्तिम दाएँ अंक को 10 में से घटाओ।'
निखिलम् सूत्र की सहायता से अंकों के समूह का भी विनकुलम् सरलतापूर्वक प्राप्त कर सकते है। अतः यह निखिलम् सूत्र दी हुई सामान्य संख्या को विनकुलम् संख्या के रूप में लिखने का एक सशक्त साधन है।
(6) Nikhilam Sutra:
Nikhilam Sutra is –
'Nikhilam Navatah Charam Dashatah' means 'Subtract each digit from 9 and the last right digit from 10.'
With the help of Nikhilam Sutra, Vinakulam of a group of numbers can be easily obtained. Hence, this Nikhilam formula is a powerful means of writing the given ordinary number in the form of Vinkulam Number.
(7) साधारण संख्या को विनकूलम् संख्या के रूप में लिखना:
किसी संख्या को विनकुलम् रूप में लिखने के लिए उस संख्या में आने वाले 5 से बड़े अंकों को उनके विनफुलम् अंकों से बदल दिया जाता है। और संख्या में जो अंक 5 से छोटे होते हैं उन्हें ज्यों का त्यों ही लिख दिया जाता है।
अब हम विनकुलम् अंक लिखने की पूरी विधि का विस्तार से वर्णन करेंगे।
(7) Writing an ordinary number in the form of Vinkulam number:
To write a number in Vinkulum form, the digits greater than 5 in that number are replaced with their Vinkulum digits. And the digits in the number which are less than 5 are written as they are.
Now we will describe in detail the complete method of writing Vinkulam numbers.
किसी अंक का विनकुलम् ज्ञात करना :
5 से बड़े जिस अंक का विनकुलम् ज्ञात करना हो तो उसका ’10 से विचलन’ ज्ञात कर लेते हैं। इस प्रकार जो ऋणात्मक अंक आता है। उसी को हम उस संख्या का विनकुलम अंक कहते हैं।
To find the vinculum of a number:
If we want to find the vinkulam of a number greater than 5, then its 'deviation from 10' is found. In this way, the negative soul number that comes, is a Vinkulam number.
Important Notes -
If there is no digit on the left side of the number used to find Vinkulam, then zero is written there. i.e. 0+1=1
उदाहरणार्थ
संख्या 94 या 094 को विनकुलम् रूप में लिखिए।
अंक 9 का विनकुलम् (अंक) = •0(9–10)4
अंक 9 के बायीं ओर 0 में 1 जोड़ने पर,
0+1=1
अतः
94=11'4
संक्षेप में
94 = 094 = (0+1)(9–10)4=1(–1)4=11'4
for example
Write the number 94 or 094 in Vinkulam form.
Vinkulam (digit) of number 9 = •0(9–10)4
By adding 1 to 0 on the left side of the number 9,
0+1=1
Therefore
94=11'4
in short
94 = 094 = (0+1)(9–10)4=1(–1)4=11'4
उदाहरण –
* अंक 6 का विनकुलम् ज्ञात करना।अंक 6 का 10 से विचलन = 6 – 10 = –4
अंक 6 का विनकुलम् = overline{4}
* अंक 7 का विनकुलम् ज्ञात करना।
अंक 7 का 10 से विचलन = 7 – 10 = –3
अंक 7 का विनकुलम् = overline{ 3}
* अंक 8 का विनकुलम् ज्ञात करना।
अंक 8 का 10 से विचलन = 8 – 10 = –2
अंक 8 का विनकुलम् = overline{2}
इसी प्रकार,
* अंक 9 का विनकुलम् ज्ञात करना।
अंक 9 का 10 से विचलन = 9 – 10 = –1
अंक 9 का विनकुलम् = overline{1}
* To find Vinkulam of number 6.
Deviation of number 6 from 10 = 6 – 10 = –4
Vinkulam of number 6 = overline{4}
* To find Vinkulam of number 7.
Deviation of number 7 from 10 = 7 – 10 = –3
Vinkulam of digit 7 = overline{ 3}
* To find Vinkulam of number 8.
Deviation of number 8 from 10 = 8 – 10 = –2
Vinkulam of digit 8 = overline{2}
Similarly,
* To find Vinkulam of number 9.
Deviation of number 9 from 10 = 9 – 10 = –1
Vinkulam of digit 9 = overline{1}
अंक 6 का विनकुलम् = –4
अंक 7 का विनकुलम् = –3
अंक 8 का विनकुलम् = –2
अंक 9 का विनकुलम् = –1
Thus we find that 0, 1, 2, 3, 4 and 5 do not have vinculum, only 6, 7, 8 and 9 numbers greater than 5 have vinculum.
Vinkulam of number 6 = –4
Vinkulam of number 7 =–3
Vinkulam of number 8 =–2
Vinkulam of number 9 =–1
वैदिक गणित में प्रयुक्त होने वाली संख्याओं में सभी अंक 5 या 5 से छोटे रखे जाते हैं। अतः संख्या में जो भी अंक 5 से बड़े ( 6, 7, 8, 9 ) होते हैं, उन सभी ( 6, 7, 8, 9 ) अंकों के स्थान पर उनके विनकुलम् अंक रख देते हैं।
6 का विनकुलम् अंक –4,
7 का विनकुलम् अंक –3 ,
8 का विनकुलम् अंक –2,
9 का विनकुलम् अंक –1
We used and kept the digits smaller than 5 or in the form of 1, 2, 3, 4, 5 or less than 5 in Vedic maths.
Therefore, whatever digits are greater than 5 (6, 7, 8, 9) in the number, in place of all those (6, 7, 8, 9) digits, their Vinkulam digits are written.
Vinkulam of 6 is –4,
Vinkulam of 7 is –3,
Vinkulam of 8 is –2,
Vinkulam of 9 is –1.
किसी संख्या को विनकुलम् के रूप में लिखने के लिए उस संख्या में आने वाले 5 से बड़े अंकों को उनके विनकुलम् अंकों में बदल देते हैं। 5 से छोटे अंकों को ज्यों का त्यों लिखते हैं। अब भिन्न-भिन्न उदाहरणों के माध्यम से पूरी विधि को सीखेंगे –
एक अंक के सामान्य अंकों के विनुकुलम अंक बनाना हम सीख चुके हैं।
दो अंकों के सामान्य अंको को विनकुलम अंको में बदलने के नियम।
नियम नंबर 1
संख्याओं को देखो तथा 5 से बड़े अंको को ब्रैकेट ( ) में लिखो।
नियम नंबर 2
यदि ब्रैकेट ( ) में केवल एक अंक है तो उसे 10 में से घटाओ और उससे आगे वाले अंक में 1 जोड़
Converting ordinary number to Vinkulam number:
To write a number in Vinkulam form, the digits greater than 5 appearing in that number are changed to their Vinkulam digits. Numbers less than 5 are written as they are. Now we will learn the whole method through different examples.
We have learned to make vinukulam digits of common digits of a digit.
Rules for converting two digit normal numbers into Vinculum numbers.
Rule Number 1
Look at the numbers and put the digits greater than 5 in brackets ( ).
Rule Number 2
If there is only one digit in brackets ( ), subtract it from 10 and add 1 to the digit next to it.
प्रकार 1
जब पूर्वोत्तम अंक अन्य अंको से के मुकाबले पांच या पांच से छोटे हों तो।
Type 1
Where the Purvotmanka is less than 5 than the other's.
* 18 का विनकुलम लिखिए।
* Write the vinculum of 18.
Sol.
18 = 1(8) = 1(8–10) = •1 (–2)
= 2 2'
* 27 का विनकुलम लिखिए।
* Write the vinculum of 27.
Sol.
27 = 2(7) = 2(7–10) = •2(–3) = 3 3'
* 46 का विनकुलम लिखिए।
* Write the vinculum of 46.
Sol.
46 = 4(6) = 4(6–10) = •4(–4) = 5 4'
प्रकार 2
जब पूर्वोत्तम अंक अन्य अंको के मुकाबले पांच या पांच से बड़े हों तो।
Type 2
Where the Purvotmanka is more than 5 than the other's.
* 89 का विनकुलम लिखिए।
* Write the vinculum of 89.
Sol.
089 = 0(89)
निखिलम नवत: चरमं दशत: नियम से।
By Nikhilam Navatah Charam Dashatah Sutra.
= •0(8–9) (9–10)= 1(–1)(–1) = 1 1' 1'
* 76 का विनकुलम लिखिए।
* Write the vinculum of 76.
Sol.
076 = 0(76)
निखिलम नवत: चरमं दशत: नियम से।
By Nikhilam Navatah Charam Dashatah Sutra.
= •0(7–9) (6–10)= 1(–2)(–4) = 1 2' 4'
तीन अंकों के सामान्य अंको को विनकुलम अंको में बदलने के नियम।
नियम नंबर 1
संख्याओं को देखो तथा 5 से बड़े अंको को ब्रैकेट ( ) में लिखो।
नियम नंबर 2
यदि ब्रैकेट ( ) में केवल एक अंक है तो उसे 10 में से घटाओ और उससे आगे वाले अंक में 1 जोड़
प्रकार 1 – जब केवल इकाई का अंक पांच से बड़ा हो।
जैसे
* 318 का विनकुलम लिखिए।
Write the vinculum of 318.
Sol.
318 = 31(8) = 31(8–10) = 3•1(–2) = 32 2'
* 247 का विनकुलम लिखिए।
Write the vinculum of 247.
Sol.
247 = 24(7) = 24(7–10) = 2•4(–3) =25 3'
* 145 का विनकुलम लिखिए।
Write the vinculum of 145.
Sol.
146 = 14(6) = 14(6–10) = 1•4(–4) = 15 4'
प्रकार 2
* 189 का विनकुलम लिखिए।
Write the vinculum of 189.
Sol.
189 = 1(89)
निखिलम नवत: चरमं दशत: नियम से।
By Nikhilam Navatah Charam Dashatah Sutra.
= •1(8–9) (9–10)= 2(–1)(–1) = 2 1' 1'
* 276 का विनकुलम लिखिए।
Write the vinculum of 276.
Sol.
276 = 2(76)
निखिलम नवत: चरमं दशत: नियम से।
By Nikhilam Navatah Charam Dashatah Sutra.
= •2(7–9) (6–10)= 3 2' 4'
किसी भी बड़ी संख्या का विनकुलम लिखना
* 26786 का विनकुलम लिखिए।
Write the vinculum of 26786.
Sol.
26786 = 2(6786)
निखिलम नवत: चरमं दशत: नियम से।
By Nikhilam Navatah Charam Dashatah Sutra.
= •2(6–9) (7–10)(8–9) (6–10)
= 3(–3)(–3)(–2) (–4)
= 3 3' 3' 2' 4'
संख्या 681786 को विनकुलम् रूप में लिखना।
681786
= (68)1(786)
= 0(68)1(786)
= •0(68)•1(786)
= 1(6–9)(8–10) 2(7–9)(8–9)(6–10)
= 1(–3)(–2) 2 (–2)(–1)(–4)
= 1 3' 2' 2 2' 1' 4'
अंक 6 का बिनकुलम् = –4 या 4'
अंक 7 का विनकुलम् –2 या 2'
समूह (8) का विनकुलम् ज्ञात करना :
अंक 8 का 10 से विचलन लेने पर,
अंक 8 का वितकुलम् = –2 या 2'
समूह (9) का विनकुलम् ज्ञात करना :
अंक 9 का 10 से विचलन लेने पर,
अंक 9 का विनकुलम् = –1 या 1'
अब प्रत्येक समूह में आने वाले अंकों के स्थान पर उनके वितकुलम् अंक रख देंगे तथा प्रत्येक समूह के बायीं ओर स्थित अंक के मान में एक की बुद्धि कर देंगे।
अतः विनकुलम् रूप में,
1918176 = 21'22'22'4'
Example 2.
Write the number-1918176 in Vinkulam form.
Given number = 1918176=1(9)1(8)1(76)
Here three groups of numbers greater than 5 are formed (9), (8) and (76).
To find the vinculum of group (76):
By taking the deviation of the right side digit 6 by 10 and the deviation of the second digit 7 by 9.
Binakulam of number 6 = –4 or 4'
Vinkulam of number 7 –2 or 2'
To find Vinkulam of group (8):
Taking deviation of number 8 from 10,
Vitakulam of number 8 = –2 or 2'
To find Vinkulam of group (9):
Taking the deviation of the number 9 from 10,
Vinkulam of number 9 = –1 or 1'
Now in place of the digits appearing in each group, their Vitakulam digits will be placed and the value of the digit located on the left side of each group will be increased by one.
Hence in Vinakulam form,
1918176 = 21'22'22'4'
संक्षेप में उक्त गणना इस प्रकार की जा सकती है
In short the above calculation can be done as follows-
1918176 = 1(9)1(8)1(76)
=(•1) (9-10)(•1)(8-10)(•1) [(7-9)(6-10)]
=2(–1)2(–2)2[(–2)(–4)]
=21' 2 2' 2 2' 4'
🌺🌺🌺🌺🌺🪷🪷🪷🪷🪷🌺🌺🌺🌺🌺
विनकुलम् संख्याएँ :
वे संख्याएँ जिनमें धनात्मक तथा ऋणात्मक दोनों प्रकार के अंक प्रयुक्त होते हैं, विनकुलम् संख्याएँ कहलाती हैं।
निखिलम् सूत्र के द्वारा सामान्य संख्याओं को आसानी से विनकुलम संख्या में बदला जा सकता है। :
निखिलम सूत्र है
निखिलम नवत: चरमं दशत: ।
अर्थात
‘प्रत्येक अंक को 9 में से तथा अंतिम दाएँ अंक (इकाई) को 10 में से घटाओ।’
इस सूत्र की सहायता से सामान्य संख्याओं को विनकुलम् संख्याओं में आसानी से बदल सकते हैं।
In other words ‘Subtract each digit from 9 and the last right digit (unit) from 10.’ With the help of this formula, we can easily convert normal numbers into Vinkulam numbers.
B. Conversion of vinculum number into general numbers
The process of conversion is exactly reverse to the already what we have done earlier. Rekhanks are converted by Nikhilam where as other digits by ‘Ekanyunena’ sutra.
ॠणांक (विनकुलम्) संख्या को सामान्य संख्या में बदलना
1. ॠणांक अंक का धनात्मक मान लेते हैं। ॠणांक के ऊपर शिरो रेखा की चिन्ता नही करते हुए चरमं अंक को 10 में से घटाते हैं।
2. निखिलम् अंक को 9 में से घटाते हैं, अथवा इस मान का परम मित्र लिखते हैं।
3. ॠणांक अंक के पूर्व अंक पर एकन्यून चिन्ह लगाते हैं।
* 2 2' का साधारण रूप लिखिए।
* Write the normal number from vinculum 22' .
Sol.
2 2' = *2 (10– 2) = 1(8) = 18
यह एक साधारणस नियम फॉलो करना है। उसके दहाई के अंक में शून्य लगाकर विनुकुलम अंक को घटा दो।
जैसे 2 2' में दहाई का अंक 2 है अतः उसे शून्य लगाकर बीस (20) बना लो और उसमें से विनुकुलम अंक घटा दो (20 –2 = 18) प्राप्त हो गया सामान्य अंक।
* 3 3' का साधारण रूप लिखिए।
* Write the normal number from vinculum 33'.
Sol.
3 3’ = *3(10 – 3) = 2(7) = 27
यह एक साधारणस नियम फॉलो करना है। उसके दहाई के अंक में शून्य लगाकर विनुकुलम अंक को घटा दो।
जैसे 3 3' में दहाई का अंक 2 है अतः उसे शून्य लगाकर 30 बना लो और उसमें से विनुकुलम अंक घटा दो (30 –3 = 27) प्राप्त हो गया सामान्य अंक।
* 5 4' का विनकुलम लिखिए।
* Write the normal number from vinculum 54'.
Sol.
5 4' = *5(10 –4 ) = 4(6) = 46
यह एक साधारणस नियम फॉलो करना है। उसके दहाई के अंक में शून्य लगाकर विनुकुलम अंक को घटा दो।
जैसे 5 4' में दहाई का अंक 5 है अतः उसे शून्य लगाकर 50 बना लो और उसमें से विनुकुलम अंक घटा दो (50 –4 = 46) प्राप्त हो गया सामान्य अंक।
* 4 3' 2' का विनकुलम लिखिए।
हल–
4 3' 2' = *4(9 –3 )(10–2) = 3(6)(8) = 368
Or
400 –32 = 368
* Write the normal number from vinculum of 12'.
Sol.
1 2' = *1(10 –2) = 0(8) = 8
Or
10–2 = 8
Example:
* Write the normal number from vinculum of 33'5'.
Sol.
33'5' = *3(9 –3)(10–5) = 2(6)(5) = 265
Or
300–35 = 265
Example:
* Write the normal number from vinculum of 34'56'.
Sol.
34'56' = *3(10 –4)*5(10–6) = 2(6)4(4) = 2644
Or
(30–4)(50–6)=2644
Example
* Write the normal number from vinculum of 33'44'.
Sol.
33'44' = *3(10 –3)*4(10–4) = 2(7)3(6) = 2736
Or
(30–3)(40–4)=2736
Example:
Example:

ॠणांक (विनकुलम्) संख्या को सामान्य संख्या में बदलना-
1. ॠणांक अंक का धनात्मक मान लेते हैं।
2. इस मान का परम मित्र लिखते हैं।
3. ॠणांक अंक के पूर्व अंक पर एकन्यून चिन्ह लगाते हैं।
Example:
| संकेत 1. दहाई सथान के ॠणात्मक अंक 2. 3. |
निखिलम् विधि द्वारा ॠणांक (विनकुलम्) संख्या को सामान्य संख्या में बदलना-
1. ॠणांक के ऊपर शिरो रेखा की चिन्ता नही करते हुए चरमं अंक को 10 में से घटाते हैं।
2. शेष निखिलम् अंकों को 9 में से घटाते हैं।
3. शेषफल से पूर्व अंक पर एक न्यून चिन्ह लगाते हैं।
Example:
| संकेत 1. ॠणांक के ऊपर शिरो रेखा की चिन्ता नही करते हुए चरमं अंक को 10 में से घटाते हैं, 10-2=8 2. निखिलम् अंक को 9 में से घटाते हैं, 9-3=6 3. 4 पर एक न्यून चिन्ह लगाते हैं। |
It is interesting to see that the conversions can be shown in many different ways.
Example: 87 को निम्न प्रकार से व्यक्त किया जा सकता हैं।

A. Addition and subtraction using vinkulam
Adding a bar digit or Rekhank to a digit means the digit is subtracted.
किसी रेखांक को किसी धनात्मक अंक में जोड़ने का मतलब घटाना होता हैं।
Example:
3 + 2' = 1
5 + 2' = 3
4 + 4' = 0
B. Subtracting a bar digit or Rekhank to a digit means the digit is added.
किसी रेखांक को किसी धनात्मक अंक में से घटाने का मतलब जोड़ना होता हैं।
Example:
3 – 2' = 5
2 – 2' = 4
6 – 2' = 8
3 – 3' = 6
C. Multiplication using rekhank
* Product of two positive digits or two negative (Rekhanks) digits is always positive.
दो धनात्मक या ॠणात्मक संख्याओं का गुणनफल हमेशा धनात्मक संख्या होती हैं।
Example:
3' × 3' = 9
3 × 3 = 9
2' × 3' = 6
2 × 3 = 6
3' × 4' = 12
3 × 4 = 12
* Product of one positive digit and one Rekhank is always negative or Rekhank.
एक धनात्मक तथा एक रेखांक संख्या का गुणनफल हमेशा ॠणात्मक या रेखांक संख्या प्राप्त होती हैं।
Example:
3 × 3' = 9'
3' × 3 = 9'
2' × 3 = 6'
2 × 3' = 6'
3 × 4' = 12'
3' × 4 = 12'
D. Division using rekhank
Division of one positive by another positive or division of one Rekhank by another Rekhank is always positive.
किसी धनात्मक संख्या को धनात्मक संख्या से या किसी ॠणात्मक संख्या को ॠणात्मक संख्या से भाग करने पर हमेशा धनात्मक संख्या होती हैं।
Example:
3' ÷ 3' = 1
6 ÷ 3 = 2
12' ÷ 3' = 4
12 ÷ 4 = 3
21' ÷ 3' = 7
32 ÷ 4 = 8
Division of a positive by a Rekhank or vice versa or inverse is Rekhank or negative.
किसी धनात्मक संख्या को ॠणात्मक संख्या से या किसी ॠणात्मक संख्या को धनात्मक संख्या से भाग करने पर हमेशा ॠणात्मक संख्या या रेखांक संख्या प्राप्त होती हैं।
Example:
3' ÷ 3 = 1'
6 ÷ 3' = 2'
12' ÷ 3 = 4'
12 ÷ 4' = 3'
21' ÷ 3 = 7'
32 ÷ 4' = 8'
2. Vinculum Numbers:
Vinculum means bar(line) present over the symbol/digit.
Sanskrit Name:
विनक्ल्म्
English Translation:
Complement of a number.
Vinculum Process or Vinculum Numbers are the very basics of Vedic Mathematics.
Vinculum Numbers is concept used in Vedic Mathematics and are those numbers which have atleast 1 digit which is negative (having bar over them). Also called as Bar Numbers.
As seen earlier Normal Number can be written as
2345 = 2000 + 300 + 40 + 5
Similarly Vinculum Numbers can be written as and can be converted to normal numbers as below:
- complement with a Bar over it.
- (a).If next digit is >= 5, take its 9’s complement with a Bar over it & continue this till a digit < 5 is obtained.
(b). Increment <5 digit by 1. - Continue (1) and (2) till complete number is covered.
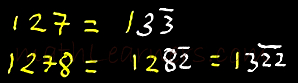
Subtraction using Vedic Mathematics:
Most of us have difficulty and uncertainty whenever we need to do subtraction, especially when it comes to subtraction of larger digits from smaller digits.
Vedic Mathematics’s Vinculum process can also be used for Subtracting 2 numbers. (How ?? watch my below Video “Vedic Mathematics -1 (Vinculum 1of3)”).
Process (R –> L):
- If bigger digit is to be subtracted from smaller digit, then just perform Bigger digit – Smaller digit and write bar over it.
- If smaller digit is to be subtracted from bigger digit then carry usual method.
- In final answer (Vinculum number) convert to normal number using Vinculum process.
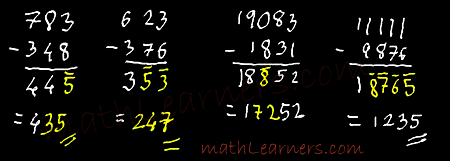
Multiplication and Division examples in Vedic Maths which uses Vinculum Process will be seen in respective topics.
3. Quotient and Remainders:
This is another important concept of Vedic Mathematics. We will follow the below formula and the concept that Remainder is ALWAYS < Divisor.
Dividend = Quotient x Divisor + Remainder
Examples:
33 ÷ 6 = 5/3 … where 5 -> Quotient & 3 -> Remainder
34 ÷ 6 = 5/4 … where 5 -> Quotient & 4 -> Remainder
35 ÷ 6 = 5/5 … where 5 -> Quotient & 5 -> Remainder
36 ÷ 6 = 6/0 … where 6 -> Quotient & 0 -> Remainder
So on observation we can say that the Remainder can never be >= Divisor.
But in Vedic mathematics in some examples depending on some criteria we need to play with Quotients and Remainders i.e. use Remainder >= Divisor for carrying out the process. But the in final answer Remainder can never be >= Divisor.
Thus for carrying out the process above examples (from bottom to top) can also be written as: ( ( watch my below Video “Vedic Mathematics -4 (Playing with Quotients and Remainders)”).)
36 ÷ 6 = 5/6 OR 4/12 OR 3/18 and so on.
35 ÷ 6 = 4/11 OR 3/17 and so on.
And vice versa for calculating final answer(Remainder can never be >= Divisor).
If we obtained Remainder(R) which is >= Divisor(D), we divide R by D and corresponding obtained quotient is added with obtained Q and new remainder becomes our R.
Lets say we obtained Q=4 & R=12, and D used was 11. As R > D, Apply above rule.
So Actuals are Q= 5 and R=1. Q=4 & R=18, and D used was 6. As R > D,
Apply above rule. So Actuals are Q= 7 and R=0.aring is caring!
Basics of Vedic Mathematics:
- Place Value System
- Vinculum Numbers (English Meaning: Complement of a Number).
- Work with Quotients & Remainders.



Post a Comment
Post a Comment