विनजीत वैदिक अंकगणित पुस्तक || 1 || अध्याय 21.00 || घन; उसके गुण एवं सूत्र

विनजीत वैदिक अंकगणित पुस्तक || 1 || अध्याय 21.00 || घन; उसके गुण एवं सूत्र

लेखक

ॐ जितेन्द्र सिंह तोमर

(M.A., B. Ed., MASSCOM, DNYS )

(Specialist in Basic and Vedic Maths)

🌺🌺🌺🪷🪷 विनजीत वैदिक गणित 🪷🪷🌺🌺🌺

घन – एक निश्चित संख्या के तीन बार गुणन से  प्राप्त गुणनफल उस संख्या का घन कहलाता है। इन संख्याओं को पूर्ण घन (perfect cubes) या घन संख्याएँ (cube numbers) भी कहते हैं।

a का घन = a x a x a = a³

★ वर्तमान गणित में a × a × a को a³ के रूप में व्यत्क्त करने का श्रेय “रेने द कार्टे” को दिया जाता है।

★ In current mathematics, the credit of expressing as, a × a × a = a³ is given to “Rene de Carte”.

★ The cube of a number a is denoted by a³ and the cube root by ∛a.

★ किसी संख्या a के घन को a³ से तथा घनमूल को ∛a से सूचित किया जाता है।

Cube – The product obtained by multiplying a certain number three times is called the cube of that number. These numbers are also called perfect cubes or perfect cube numbers.

Cube of a = a x a x a = a³

घन की ज्यामितीय परिभाषा

ऐसी ठोस आकृति, जिसकी सभी भुजाएँ बराबर होती हैं। उसे घन कहा जाता है। 

जब किसी वर्ग के प्रत्येक किनारे की लम्बाई के बराबर उसके तलके लम्बवत रखकर जो चौकोर आकृति प्राप्त किया जाता है, उसे घन कहा जाता है। ज्यामिति में, घन एक 3D ठोस वस्तु है जिसमें छह वर्गाकार फलक होते हैं और एक घन की सभी भुजाएँ समान लंबाई की होती हैं।

घन के प्रत्येक सतह का क्षेत्रफल = a²

घन की धारिता या आयतन = a³

Geometric Definition Of Cube

A solid shape whose all sides are equal. It is called a cube.

When a square shape is obtained by keeping its bottom perpendicular to the length of each edge of a square, it is called a cube. In geometry, a cube is a 3D solid object that has six square faces and all sides of a cube are of equal length.

Area of each surface of the cube = a²

Capacity or volume of cube = a³

घन का टेबल (1 से 30 तक)

Cube Table (1 to 30)

संख्या          घन              संख्या              घन

Number    Cube         Number        Cube

(1)³               1              (16)³           4096

(2)³               8              (17)³           4913

(3)³             27              (18)³           5832

(4)³             64              (19)³           6859

(5)³           125              (20)³           8000

(6)³           216              (21)³            9261

(7)³           343              (22)³          10648

(8)³           512              (23)³          12167

(9)³           729              (24)³          13824

(10)³       1000              (25)³          15625

(11)³       1331              (26)³          17576

(12)³       1728              (27)³          19683

(13)³       2197              (28)³          21952

(14)³       2744               (29)³         24389

(15)³       3375               (30)³         27000

उपरोक्त सारणी से निम्न परिणाम और महत्वपूर्ण तथ्य प्राप्त होते हैं:

★ प्राकृत संख्या m पूर्ण घन कहलाती है, यदि वह किसी प्राकृत संख्या n का घन हो।

यानि m = n³ हो , तो m एक पूर्ण घन है , जहाँ m और n प्राकृत संख्याएँ हैं।

★ किसी संख्या के अंतिम अंक और घन संख्या के अंतिम अंक में कोई परिवर्तन नहीं होगा, अतः 0, 1, 4, 5, 6, 9 के घन के इकाई स्थान पर क्रमशः 0, 1, 4, 5, 6, 9  होते हैं।

परंतु बाकी बचे 2 को 8 से और 8 को 2 से और 3 को 7 से और 7 को 3 से बदल देते हैं। 

★ वैदिक गणित की भाषा में कहें तो 7 और 3 के परिणाम एक दूसरे के पूरक होते हैं।

The following results and important facts are obtained from the above table:

★ A natural number m is called a perfect cube if it is the cube of some natural number n.

That is, if m = n³, then m is a perfect cube, where m and n are natural numbers.

★ There will be no change in the last digit of a number and the last digit of a cube number, hence at the unit place of the cube of 0, 1, 4, 5, 6, 9, we get 0, 1, 4, 5, 6, 9 respectively.

But the remaining 2 is replaced by 8 and 8 is replaced by 2 and 3 is replaced by 7 and 7 is replaced by 3.

★ In the language of Vedic mathematics, the results of 7 and 3 is complement of each other.

पूर्ण घन संख्या का अंतिम अंक      घन का अंतिम अंक

Last digit of 

perfect cube No.                     Last digit of cube

                 0                                  0

                 1                                  1

                 2                                  8

                 3                                  7

                 4                                  4

                 5                                  5

                 6                                  6

                 7                                  3

                 8                                  2

                 9                                  9

★ जब सम संख्याओं को घन किया जाता है, तो परिणाम एक सम संख्या होगी। उदाहरण के लिए, 2³ = 8, 4³ = 64

★ When even numbers are cubed, the result will be an even number. For example, 2³ = 8, 4³ = 64

★ जब विषम संख्याओं को घन किया जाता है, तो परिणाम एक विषम संख्या होगी। उदाहरण के लिए, 3³ = 27, 5³ = 125

★ When odd numbers are cubed, the result will be an odd number. For example, 3³ = 27, 5³ = 125

★ 1 से 1000 तक केवल दस पूर्ण घन है। 

★ There are only ten perfect cubes from 1 to 1000.

★ पूर्ण घन संख्याएँ धनात्मक या ऋणात्मक दोनों पूर्णांक हो सकती हैं। उदाहरण के लिए, 8 और –8 दोनों क्रमशः 2 और – 2 के पूर्ण घन हैं।

★ Perfect cube numbers can be both positive or negative integers. For example, both 8 and –8 are perfect cubes of 2 and – 2 respectively.

★ पूर्ण घनों को लगातार विषम संख्याओं के योग के रूप में व्यक्त किया जा सकता है। 

1 = 1  = 1³

3 + 5 = 8 = 2³

7+ 9 + 11 = 27  = 3³

13 + 15 + 17 + 19 = 64 =4³

 21 + 23 + 25 +27 + 29 = 125 = 5³

★ Perfect cubes can be expressed as the sum of consecutive odd numbers.

1 = 1 = 1³

3 + 5 = 8 = 2³

7+ 9 + 11 = 27 = 3³

13 + 15 + 17 + 19 = 64 =4³

  21 + 23 + 25 +27 + 29 = 125 = 5³

★ निम्नलिखित प्रतिरूप को देखिए :

2³–1³ =1+2x1x3

3³–2³ = 1+3×2×3

4³ –3³ = 1+4x3x3

प्रतिरूप देखकर पता चलता है कि

b³ –a³ = 1 + b × a × 3

★ Look at the following pattern:

2³–1³ =1+2x1x3

3³–2³ = 1+3×2×3

4³ –3³ = 1+4x3x3

Looking at the pattern it is clear that

b³ –a³ = 1 + b × a × 3

उपरोक्त प्रतिरूप का प्रयोग करते हुए, निम्नलिखित के मान ज्ञात कीजिए :

Using the above model, find the values of the following:

(i) 7³–6³

(ii) 11³ –10³

(iii) 12³–11³

(iv) 21³–20³

(v) 27³–26³

(vi) 42³ –41³

(vii) 50³–49³

(viii) 51³–50³

🌺🌺🌺🪷🪷 विनजीत वैदिक गणित 🪷🪷🌺🌺🌺

घन निकलने की विधि: 

वर्ग की तरह घन भी कई प्रकार से निकाले जाते है।

01. पारंपरिक गुणन विधि (तीन बार गुणा द्वारा)

02. पारंपरिक सूत्र विधि द्वारा 

03. अनुमान या विलोकनम विधि द्वारा 

04. यावदूनी तावदूनी सूत्र द्वारा 

05. आनयूरूपेण विधि द्वारा 

06. निखिलम विधि द्वारा 

07. एकाधिकेन विधि द्वारा 

Method of getting cube:

Like squares, cubes are also calculated in many ways.

01. Traditional multiplication method (by multiplying three times)

02. By traditional formula method

03. By estimation or visualization method

04. Yavaduni by Taavaduni Sutra

05. By aanayooroopen method

06. By Nikhilam method

07. By one more (ekaadhiken vidhi) method

🌺🌺🌺🪷🪷 विनजीत वैदिक गणित 🪷🪷🌺🌺🌺

01. पारंपरिक गुणन विधि (तीन बार गुणा द्वारा)

संख्या N का घन = N × N × N

                        = N³

                        

01. Traditional multiplication method (by multiplying three times)

Cube of number N = N × N × N

                         = N³

🌺🌺🌺🪷🪷 विनजीत वैदिक गणित 🪷🪷🌺🌺🌺

02. पारंपरिक सूत्र विधि

02.Traditional formula method

a³ = a³ 

a³ = a³ – a + a
= a (a² – 1) + a
= (a – 1) × a × (a+1) + a

उदाहरण –> 11 का घन बताएं
हल:- यहाँ a = 11 है अतः इसके पूर्ववत और अगली संख्या क्रमशः 10 और 12 होंगे। सबसे पहले आप 10 , 11 एवं 12 को गुणा करें और परिणाम में 11 जोड़ दें।

Example –> What is the cube of 11.

Sol. - Here a = 11, hence its previous and next numbers will be 10 and 12 respectively. First of all, multiply 10, 11 and 12 and add 11 to the result.

                                 11                         

     ↓                           ↓                          ↓        +

(a – 1)          ×          a           ×        (a+1)     +     a

(11 – 1)        ×         11          ×       (11+1)    +   11

= 10×11×12+11

= 1320 +11

= 1331

उदाहरण–> 25 का घन बताएं
हल:- यहाँ a = 25 है अतः इसके पूर्ववत और अगली संख्या क्रमशः 24 और 26 होंगे. सबसे पहले आप 24 , 25 एवं 26 को गुणा करें और परिणाम में 25 जोड़ दें.

Example –> What is the cube of 25?

Sol.- Here a = 25, hence its previous and next numbers will be 24 and 26 respectively. First of all, multiply 24, 25 and 26 and add 25 to the result.

= (a – 1) × a × (a+1) + a

=24 × 25 × 26 + 25

= 15600 + 25

= 15625

🌺🌺🌺🪷🪷 विनजीत वैदिक गणित 🪷🪷🌺🌺🌺

03. अनुमान या विलोकनम विधि द्वारा 

03. By estimation or visualization method

🌺🌺🌺🪷🪷 विनजीत वैदिक गणित 🪷🪷🌺🌺🌺

04. यावदूनी तावदूनी सूत्र द्वारा 

जहां संख्या = N

आधार = Base

आधार से विचलन = d

         चरण 1        चरण 2                         चरण 3

N³ = (N + d×2) / [(N + d×2)–base] d /  d³

चरण 1 –> (N + d×2)

चरण 2 –> [(N + d×2)–base] d

चरण 3 –> d³

04. Yavaduni by Taavaduni Sutra

where number = N

Base = Base

Deviation from base = d

       Step 1              Step 2                      Step 3

N³ = (N + d×2) / [(N + d×2)–base] d / d³

Step 1 –> (N + d×2)

Step 2 –> [(N + d×2)–base] d

Step 3 –> d³

103 का घन ज्ञात करो।

Find the cube of 103.

Base = 100

deviation = 3

चरण –> (1) N + d×2 

= 103 +3×2 = 103 +6 = 109

103, 100 से 3 अधिक है, अतिरिक्त अधिक्य (3) को 2 से गुणा करें और संख्या के साथ इस गुणनफल को जोड़ें। 

चरण –> (2a) new d of NN

 = New d (n.d) of 109 = 9

चरण –> (2b) n.d × o.d

= 9 × 3 = 27

अब 103 के मूल आधिक्य (3) को नये 109 के आधिक्य (9) को आपस में गुणा करके चरण –> (1) बनाएं।

चरण –> (3) (d)³

3³ = 27

तीसरे चरण में 103 के मूल आधिक्य (3) का घन लें। 

संक्षेप में

= चरण –> (1) /चरण –> (2a &b) /चरण –>3

= 103 +3×2 / 9 × 3 / 3³

=109/27/27

103³ = 1092727

Ex. Find the cube of 103.

Base = 100

deviation = 3

Step –> (1) N + d×2

= 103 +3×2 = 103 +6 = 109

103 is 3 more than 100, multiply the excess (3) by 2 and add this product to the number.

Step –> (2a) new d of NN

  = New d (n.d) of 109 = 9

Step –> (2b) n.d × o.d

= 9 × 3 = 27

Now multiply the original excess (3) of 103 with the excess (9) of new 109 and make step –> (1).

Step –> (3) (d)³

3³ = 27

In the third step, take the cube of the original excess (3) of 103.

In Short

= Step –> (1) /Step –> (2a &b) /Step –>3

= 103 +3×2 / 9 × 3 / 3³

=109/27/27

103³ = 1092727

उदाहरण –> 1004 का घन ज्ञात करो।

Base = 100

deviation = 4

चरण –> (1) N + d×2 

= 1004 +4×2 = 1004 +8 = 1012

1004, 1000 से 4 अधिक है, अतिरिक्त अधिक्य (4) को 2 से गुणा करें और संख्या के साथ इस गुणनफल को जोड़ें। 

चरण –> (2a) new d of NN

 = New d (n.d) of 1012 = 12

चरण –> (2b) n.d × o.d

= 12 × 4 = 048

अब 1004 के मूल आधिक्य (4) को नये 1012 के आधिक्य (12) को आपस में गुणा करके चरण –> (1) बनाएं।

चरण –> (3) (d)³

4³ = 64

तीसरे चरण में 1004 के मूल आधिक्य (4) का घन लें। 

संक्षेप में

= चरण –> (1) /चरण –> (2a &b) /चरण –>3

= 1004 +4×2 / 12 × 4 / 4³

= 1012 / 048 / 064

104³ = 1012048064

Example –> Find the cube of 1004.

Base = 100

deviation = 4

Step –> (1) N + d×2

= 1004 +4×2 = 1004 +8 = 1012

1004 is 4 more than 1000, multiply the excess (4) by 2 and add this product to the number.

Step –> (2a) new d of NN

 = New d (n.d) of 1012 = 12

Step –> (2b) n.d × o.d

= 12 × 4 = 048

Now multiply the original excess (4) of 1004 with the excess (12) of new 1012 and make Step – > (1).

Step –> (3) (d)³

4³ = 64

In the third step, take the cube of the original excess (4) of 1004.

In Short

= Step –> (1) /Step –> (2a &b) /Step –>3

= 1004 +4×2 / 12 × 4 / 4³

= 1012 / 048 / 064

104³ = 1012048064

उदाहरण –> 96³ का घन ज्ञात करो।

जहां संख्या = N = 96

आधार = Base = 100

आधार से विचलन = d = –4

संख्या 96, आधार 100 से 4 कम या न्यून है।

= चरण –> (1) कमी या न्यूनता (–4) को 2 से गुणा करें और संख्या के साथ इस गुणनफल को जोड़ें। 

= 96 +–4×2 = 96 –8 = 88

चरण –> (2a) new d of NN

 = New d (n.d) of 88 = –12

चरण –> (2b) n.d × o.d

= –12 × –4 = 48

अब 96 के मूल कमी या न्यूनता (–4) को नये 88 के कमी या न्यूनता (–12) को आपस में गुणा करके चरण –> (2) बनाएं।

चरण –> (3) (d)³

(–4)³ = –64

संक्षेप में

= चरण –> (1) /चरण –> (2a &b) /चरण –>3

= 96 + (–4) × 2 / –12 × –4 / 4³

=88/48/–64

=88/47/36

Example –> Find the cube of 96³.

Where Number = N = 96

Base = Base = 100

Deviation from base = d = –4

The number 96 is 4 less or less than the base 100.

= Step –> (1) Multiply the reduction (–4) by 2 and add this product with the number.

= 96 +–4×2 = 96 –8 = 88

Step –> (2a) new d of NN

  = New d (n.d) of 88 = –12

Step –> (2b) n.d × o.d

= –12 × –4 = 48

Now multiply the original reduction or reduction (–4) of 96 by the reduction or reduction (–12) of new 88 and make step –> (2).

Step –> (3) (d)³

(–4)³ = –64

In Short

= Step –> (1) /Step –> (2a &b) /Step –>3

= 96 +(–4)×2 / –12 × –4 / 4³

=88/48/–64

=88/47/36

उदाहरण –> 996³ का घन ज्ञात करो।

जहां संख्या = N = 996

आधार = Base = 1000

आधार से विचलन = d = –4

संख्या 996, आधार 1000 से 4 कम या न्यून है।

= चरण –> (1) कमी या न्यूनता (–4) को 2 से गुणा करें और संख्या के साथ इस गुणनफल को जोड़ें। 

= 996 +–4×2 = 96 –8 = 988

चरण –> (2a) new d of NN

 = New d (n.d) of 988 = –12

चरण –> (2b) n.d × o.d

= –12 × –4 = 048 

(क्योंकि आधार 1000 है इसलिए तीन अंक लेंगे।)

अब 996 के मूल कमी या न्यूनता (–4) को नये 988 के कमी या न्यूनता (–12) को आपस में गुणा करके चरण –> (2) बनाएं।

चरण –> (3) (d)³

(–4)³ = –064

(क्योंकि आधार 1000 है इसलिए तीन अंक लेंगे।)

संक्षेप में

= चरण –> (1) /चरण –> (2a &b) /चरण –>3

= 996 +(–4)×2 / –12 × –4 / 4³

=988/048/–064

=988/047/936

Example –> Find the cube of 996³.

Where Number = N = 996

Base = Base = 1000

Deviation from base = d = –4

The number 996 is 4 less or less than the base 1000.

= Step –> (1) Multiply the reduction or diminution (–4) by 2 and add this product with the number.

= 996 +–4×2 = 96 –8 = 988

Step –> (2a) new d of NN

  = New d (n.d) of 988 = –12

Step –> (2b) n.d × o.d

= –12 × –4 = 048

(Since base is 1000 hence three digits will be taken.)

Now multiply the original deficiency or deficiency (–4) of 996 by the deficiency or deficiency (–12) of new 988 and make step –> (2).

Step –> (3) (d)³

(–4)³ = –064

(Since base is 1000 hence three digits will be taken.)

In Short

= Step –> (1) /Step –> (2a &b) /Step –>3

= 996 +(–4)×2 / –12 × –4 / 4³

=988/048/–064

=988/047/936

🌺🌺🌺🪷🪷 विनजीत वैदिक गणित 🪷🪷🌺🌺🌺

05. आनयूरूपेण विधि द्वारा –> वैदिक गणित का उपयोग करके घन ज्ञात करना।

अनुरूपयेन सूत्र वैदिक गणित में घन ज्ञात करने का शॉर्टकट है। यह किसी भी 2 अंकीय संख्या पर लागू किया जा सकता है।

05. By Aanurupena method –> Finding the cube using Vedic mathematics.

The corresponding formula is the shortcut to find the cube in Vedic mathematics. This can be applied to any 2 digit number.

(a+b)³ = a³ + 3a²b + 3ab² + b³

(a+b)³ = a³  / a²b   /  ab²    / b³

            =      2×a²b  / 2×ab²         

(a+b)³ = a³ + 3a²b + 3ab² + b³

उदहारण : 63 का घन करें |

हल : 63³ यानि 63×63×63 =?

सबसे पहले संख्या के पहले अंक का घन करें | जैसे यहाँ 6 का घन 216 है (6³= 216) अब प्रश्न संख्या के दोनों अंकों का अनुपात निकालें जिस प्रकार यहाँ 6:3 = 2: 1 है | अब प्राप्त संख्या 216 के आगे एक सीधी लाइन में 3 ओर संख्याएँ 2:1 के अनुपात: में लिखें जैसे 2:1 = 216:108 व 2:1 = 108:54 व 2:1 = 54:27

इस प्रकार हमे 4 संख्याएँ प्राप्त होती हैं 216, 108, 54 और 27 और बीच की 2 संख्याओ 108 व 54 का दोगुना उन्ही के नीचे लिखें और इनको इस प्रकार लिखें जैसे कि नीचे लिखी गयी हैं |

प्रथम चरण :

     a³     / a²b   /  ab²   / b³

    216    108        54      27

            + 216    +108               

     216      324     162      27

            250047

इस प्रकार हमे चार संख्याएँ प्राप्त होती हैं 216, 324, 162 व 27

 इनको पीछे से हल करना शुरू करें यानि 27 से तो सही उत्तर निकाल आएगा |

अंतिम अंक 27 का 7 व 2 हासिल = _ / _ / _ / 7

162 +2 (हासिल) = 164 का 4 व 16 हासिल = _ / _ / 4 / 7

324+16 (हासिल) = 340 की 0 व 34 हासिल = _ / 0 / 4 / 7

216+34(हासिल) = 250 का 250 = 250 / 0 / 4 / 7

अतः 63³ = 250047 उत्तर

Example: Cube 63.

Solution: 63³ i.e. 63×63×63 =?

First cube the first digit of the number. Like here the cube of 6 is 216 (6³ = 216) Now find the ratio of both the digits of the question number as here 6:3 = 2:1. Now write 3 more numbers in a straight line next to the number 216 in the ratio of 2:1 like 2:1 = 216:108 and 2:1 = 108:54 and 2:1 = 54:27.

In this way we get 4 numbers 216, 108, 54 and 27 and write double of the middle two numbers 108 and 54 below them and write them as follows.

First Step :

      a³ /    a²b /     ab² /     b³

     216    108        54        27

             +216     +108            

      216   324       162       27

             250047

In this way we get four numbers 216, 324, 162 and 27.

Start solving them from the back i.e. from 27 onwards the correct answer will come out.

Last digit obtained is 7 and 2 of 27 = _ / _ / _ / 7

162 +2 (achieved) = 4 of 164 and 16 achieved = _ / _ / 4 / 7

324+16 (achieved) = 0 of 340 and 34 achieved = _ / 0 / 4 / 7

216+34(Gain) = 250 of 250 = 250 / 0 / 4 / 7

Hence 63³ = 250047 Answer

12³

(a + b)² = a³    /    a²b /     ab² /     b³

(1 + 2)³ = 1³  / 1² × 2   /  1 × 2²    / 2³

I             = 1  /       2     /   4           / 8

II                            4     /   8                      

III           = 1  /       6     /    ¹2     /  8

              = 1 / 7 / 2 / 8

              = 1728

चरण 1.  हम 12 के अंकों दो भागों (1और 2) में विभक्त करेंगे और फिर उनका अर्थात 

1 और 2 का अनुपात 1:2 है.

चरण 2.  1 का घन (cube) लिखेंगे ---  1³ =1

चरण 3.  अब अंकों का अनुपात 1:2* है इसलिए दुसरे चरण में प्राप्त संख्या को 2 से गुणा* कर लिखते जायेंगे (तीन बार)--- 1  2   4   8.

चरण 4.  बीच के दो संख्याओं का दुगुना कर उन्हीं के नीचे लिख देंगे--- 2 और 4 का दुगुना 4 और 8 है.

चरण 5.अब दायें से बाएं जोड़ना है---यदि जोड़ में एक से अधिक अंक आये तो उसे उसके बाएं वाले में जोड़ देना है,जैसे 8+4=12 का 2 लिखा गया और 1 को अगले में 2+4+1=7 कर दिया गया.

यदि यह अनुपात 2:5  (=1:  5/2) होता तो पहले तो 2 का घन=2^3=8 लिखते फिर अन्य तीन के लिए 8 को 5/2 से गुणा करते=20, 20x 5/2=50,50x 5/2=125 लिखते. अगले चरण में बीच वाले का दुगुना--40 और 100.और अंत में जोड़ करने से 25 का घन मिलता. 

Step 1. We will divide the digits of 12 into two parts (1 and 2) and then divide them i.e.

The ratio of 1 and 2 is 1:2.

Step 2. Write the cube of 1 --- 1³ =1

Step 3. Now the ratio of the digits is 1:2*, hence the number obtained in the second step will be multiplied by 2* and written (three times)--- 1 2 4 8.

Step 4. Double the middle two numbers and write below them - Twice of 2 and 4 is 4 and 8.

Step 5. Now add from right to left---if there is more than one digit in the addition then it has to be added to the one on its left, like 2 of 8+4=12 is written and 1 is written in the next 2+4+1. =7 has been made.

If this ratio were 2:5 (=1: 5/2) then first we would write cube of 2 = 2^3 = 8 and then for the other three we would multiply 8 by 5/2 = 20, 20x 5/2 = 50. Write 50x 5/2=125. In the next step, double the middle one - 40 and 100. And finally by adding, we get the cube of 25.

25³ =

(a + b)² = a³    /    a²b /     ab² /     b³

(2 + 5)³ = 2³  / 2² ×5   /  2 × 5²    / 5³

             = 8  /       20    /   50          / 125

                             40    /  100               

             = 8  /      60   /    150   /  125

दायें से बाएं जोड़ने के क्रम में 8\60\150\125

= 8\60\150+12\5

= 8\60\162\5

= 8\60+16\2\5

= 8\76\2\5

= 8+7\6\2\5

= 15\6\2\5

43³

(a + b)² = a³    /    a²b /     ab² /     b³

(4 + 3)³ = 4³  / 4² ×3   /  4 × 3²    / 3³

             = 64  /       48    /   36          / 27

                               96    /   72               

             = 64  /      ¹⁴4   /    ¹⁰8     /  ²7

             = 79 / 5 / 0 / 7

             = 79507

🌺🌺🌺🪷🪷 विनजीत वैदिक गणित 🪷🪷🌺🌺🌺

(06) निखिलम् विधि से घन करना –>  वैसे तो वैदिक गणित में घन निकालने की बहुत सी विधियाँ हैं। परन्तु निखिलम् विधि सबसे सरल विधियों में से एक है।हम पाते हैं कि यह निखिलम् विधि इतनी व्यापक नही है फिर भी जिन स्थानों पर यह विधि लागू होती है; वहां हम इस विधि द्वारा उत्तर मन ही मन पलक झपकते ही बता सकते हैं | 

आप जानते ही हैं कि निखिलम् विधि गुणा, भाग व वर्ग करने में केवल उन्ही संख्याओं को हल करने में ज्यादा सक्षम है जो संख्याऐ आधार के ज्यादा करीब की होती हैं। गुणा, भाग व वर्ग के समान ही हम घन भी  निकाल सकते हैं।

(06) Calculating cube using Nikhilam method -> Actually, there are many methods of calculating cube in Vedic mathematics. But Nikhilam method is one of the simplest methods. We find that this Nikhilam method is not so widespread, yet the places where this method is applicable; There we can tell the answer in our mind in the blink of an eye by this method.

You already know that Nikhilam method is more capable in solving multiplication, division and square only those numbers which are closer to the base. Just like multiplication, division and square, we can also find cubes.

सूत्र (Formula)

(A) आधार विधि से 

संख्या + 2 × वि० / 3 × वि.² / वि.³

Formula

(A) By Base Method

(Num + 2 × d) / 3 × d² / d³

(B) उपाधार विधि से 

(उपाधार अंक) × (संख्या + 2x वि) / उपा. अंक × 3× वि०²/वि०³

(B) By sub-base Method

(Sbd)² (Num +2×d)/ 2  Sbd×3×d²/d³

16³

आधार = 10 वि. = 6

संख्या +2 + वि. / 3 × वि.² / वि.³

16³ = 16+2x6/3x62/63

       = 16+12/¹⁰8/216

       = 28/¹⁰8/²¹6

        = 4096 

16³

Base = 10 V = 6

Number +2 + V. / 3 × V.² / V.³

16³ = 16+2x6/3x62/63

        = 16+12/¹⁰8/216

        = 28/¹⁰8/²¹6

         = 4096

96³

आधार = 100 वि. = –4

संख्या +2 + वि. / 3 × वि.² / वि.³

= 96+2×(–4) / 3×(–4)² / (–4)³

= 88 / 48 / –64

= 88 / 47 / 100–64

= 88 / 47 / 36

= 884736

96³

Base = 100 V = –4

Number +2 + V. / 3 × V.² / V.³

= 96+2×(–4) / 3×(–4)² / (–4)³

= 88 / 48 / –64

= 88 / 47 / 100–64

= 88 / 47 / 36

= 884736

(B) उपाधार विधि से 

(उपाधार अंक)² × (संख्या + 2x वि) / उपा. अंक × 3× वि०² / वि०³

43³

आधार = 10; उपाधार = 10 × 4;  उपाधार अंक =  – 4

(उपाअंक)² (संख्या + 2× वि.) / उपा. अरु ×3× वि² / वि³ 

= (4²) (43+2×3)/ 4×3×3²/3³

= 16x (49) / 108 / 27

= 784 / ¹⁰8 / ²7

= 179507

(B) Substantive method

(Base digit)² × (Number + 2x V) / Sub. Digit × 3× V0² / V0³

43³

base = 10; Substrate = 10 × 4; Base digit = – 4

(sub-number)² (number + 2× ex.) / sub-number. Aru ×3× V² / V³

= (4²) (43+2×3)/ 4×3×3²/3³

= 16x (49) / 108 / 27

= 784 / ¹⁰8 / ²7

= 179507

🌺🌺🌺🪷🪷 विनजीत वैदिक गणित 🪷🪷🌺🌺🌺

07. एकाधिकेन विधि द्वारा 

घन निकलने की एक और विधि है; एकाधिकेन विधि यह थोड़ी मेहनती है लेकिन परिणाम अच्छा देती है।

07. By exclusive method

There is another method to get the cube; Ekaadhiken method: This is a bit laborious but gives good results.

(ab)³ = (a)² × •(a) / (a)² × d / 3× (a) × (b)² / (b)³

d = b × 3 –10

सूत्र = (द.अं.)² × •(द.अं.) एकाधिक / (द.अं.)² × वि० / 3× (द.अं.) × (इ.अं.)² / (इ.अं.)³

Formula = (T.d.)² × •(T.d.) / (T.d.)² × dav / 3× (T.d.) × (U.d.)² / (U.f.)³

विचलन = [(इ.अं.) ×  3] – 10

Deviation = [(U.d.) ×  3] – 10

🌺🌺🌺🪷🪷 विनजीत वैदिक गणित 🪷🪷🌺🌺🌺

67³

(ab)³ = (a)² × •(a) / (a)² × d / 3× (a) × (b)² / (b)³

d = b × 3 –10

वि. = (7 × 3)–10 = 21–10 = 11

सूत्र = (द.अं.)² × •(द.अं.) एकाधिक / (द.अ.)² × वि० / 3× (द.अं.) × (इ.अं.)² / (इ.अं.)

(ab)³ = (a)² × •(a) / (a)² × d / 3× (a) × (b)² / (b)³

(67)³ = (6)² × •(6) / (6)² × 11 / 3× (6) × (7)² / (7)³

= 6² × 7 / 6² × 11/ 3x6x49 /7 2 2 3

= 252 / 396 / 882 / 343

      ⁴⁸       ⁹¹     ³⁴

= 252 / ³⁹6 / ⁸⁸2 / ³⁴3

= 300763

67³

(ab)³ = (a)² × •(a) / (a)² × d / 3× (a) × (b)² / (b)³

d = b × 3 –10

d. = (7 × 3)–10 = 21–10 = 11

(ab)³ = (a)² × •(a) / (a)² × d / 3× (a) × (b)² / (b)³

(67)³ = (6)² × •(6) / (6)² × 11 / 3× (6) × (7)² / (7)³

= 6² × 7 / 6² × 11/ 3x6x49 /7 2 2 3

= 252 / 396 / 882 / 343

      ⁴⁸       ⁹¹     ³⁴

= 252 / ³⁹6 / ⁸⁸2 / ³⁴3

= 300763

🌺🌺🌺🪷🪷 विनजीत वैदिक गणित 🪷🪷🌺🌺🌺

संख्याओं के घन - भाग 1

यवदुनम सूत्र (जिसकी कमी जितनी भी हो, उसे उतनी ही कम करें और उस कमी का वर्ग भी निर्धारित करें) जिसका उपयोग संख्याओं का वर्ग करने के लिए किया जाता है, इसका उपयोग कुछ परिवर्तनों के साथ संख्याओं के घन खोजने के लिए भी किया जा सकता है, जैसा कि बताया गया है नीचे:

 जैसे 973 ³

Cubes of Numbers - Part 1

The Yavadunam formula (reduce the number by whatever is lacking and also determine the square of that deficiency) which is used to find the square of numbers can also be used to find the cubes of numbers with some modifications, as explained below:

e.g. 973³

1. 10 की निकटतम घात का चयन करें, इस स्थिति में यह 100 होगा
2. 100 में से 97 की कमी 3 है, अतः नयूनशेष 3 है। हम उस नयूनशेष का दोगुना लेते हैं जो 6 है। फिर हम 97 को घाटे के दोगुने से और कम करते हैं यानी 6 सेट (97– 6)=91 उत्तर के बाईं ओर के भाग के रूप में 91/
3. फिर हमने उत्पाद के मध्य भाग के रूप में नए नयूनशेष को मूल शेष (9×3 = 27) से गुणा करके 91/27 डाल दिया।
4. दाहिनी ओर, हम मूल कमी का घन –33 = –27 डालते हैं
5. इस प्रकार 973 ³ = 91/27/–27 = 912673

1. Select the nearest power of 10, in this case it would be 100.

2. The minimum of 97 from 100 is 3, so the least minimum is 3. We take twice the least minimum which is 6. Then we further reduce 97 by twice the least minimum i.e. 6 Set (97 – 6)=91 as the left side part of the answer 91/

3. Then we put 91/27 as the middle part of the product by multiplying the new least minimum by the original minimum (9×3 = 27).

4. On the right side, we put the cube of the original minimum –33 = –27

5. Thus 973³ = 91/27/–27 = 912673

उदाहरणार्थ 10063 ³

1. 10 की निकटतम घात का चयन करें, इस स्थिति में यह 1000 होगी
2. 1000 से अधिशेष 6 है, हम अधिशेष का दोगुना लेते हैं जो कि 12 है। फिर हम 1006 को अधिशेष के दोगुने से और बढ़ाते हैं अर्थात 12 सेट (1006+12)=1018 उत्तर 1018/ के बाईं ओर के भाग के रूप में
3. फिर हम नए अधिशेष को मूल अधिशेष (18×6 = 108) से गुणा करके उत्पाद के मध्य भाग 1018/108/ के रूप में रखते हैं।
4. दाहिनी ओर, हम मूल अधिशेष 63 = 216 का घन नीचे रखते हैं
5. इस प्रकार 10063 ³ = 1018/108/216 = 1018108216

For example 10063³

1. Choose the nearest power of 10, in this case it will be 1000.

2. The surplus from 1000 is 6, we take twice the surplus which is 12. Then we further increase 1006 by twice the surplus i.e. 12 Set (1006+12)=1018 as the left side part of the answer 1018/

3. Then we multiply the new surplus by the original surplus (18×6 = 108) and put down the middle part of the product 1018/108/

4. On the right side, we put down the cube of the original surplus 6³ = 216

5. Thus 10063³ = 1018/108/216 = 1018108216

 उदाहरणार्थ 10023 ³  = 1006/012/008 = 1006012008

ध्यान दें कि परिणाम के मध्य और दाएँ भाग में प्रत्येक 3 अंक चौड़ा बनाने के लिए अतिरिक्त शून्य जोड़ा गया है (चूंकि 10 की निकटतम घात जो चुनी गई है वह 1000 है)

For example 10023³ = 1006/012/008 = 1006012008

Note that extra zeros have been added to the middle and right side of the result to make it 3 digits wide (since the nearest power of 10 chosen is 1000)

 उदाहरणार्थ 1163 ³  = 148/768/4096 = 148/808/96 = 156/08/96 = 1560896

परिणाम के मध्य और दाएँ भाग को दाएँ से बाएँ ले जाने पर ध्यान दें। इनमें से प्रत्येक भाग में केवल 2 अंकों की अनुमति है क्योंकि इस मामले में चुनी गई 10 की निकटतम घात 100 है। अतिरिक्त अंकों को आगे ले जाया जाता है और उत्तर के तत्काल बाएं हाथ के हिस्से में जोड़ा जाता है।

For example 1163³ = 148/768/4096 = 148/808/96 = 156/08/96 = 1560896

Note that the middle and right-hand parts of the result are carried from right to left. Only 2 digits are allowed in each of these parts because the nearest power of 10 chosen in this case is 100. The extra digits are carried forward and added to the immediate left-hand part of the answer.

शून्य पर समाप्त होने वाली संख्या का घन

N0 का घन = N³ / 000

                = C000

10 का घन = 1³ / 000

                = 1000

20 का घन = 2³ / 000

                = 8000

70 का घन = 7³ / 000

                = 343000

Cube of a number ending in zero

Cube of N0 = N³ / 000

= C000

Cube of 10 = 1³ / 000

= 1000

Cube of 20 = 2³ / 000

= 8000

Cube of 70 = 7³ / 000

= 343000

दस के ठीक निकट वाली संख्या का घन

विधि : 1

सरल बीजगणित सूत्र (a + b)³ = a³ + 3a²b + 3ab² + b³ का उपयोग करके। 

Cube of a number just next to ten

Method : 1

Using simple algebra formula (a + b)³ = a³ + 3a²b + 3ab² + b³.

11 का घन ज्ञात कीजिए ( 11³= ? )

सरल बीजगणित सूत्र (a + b)³ = a³ + 3a²b + 3ab² + b³ का उपयोग करें। 

हम 11³ = (10 + 1 )³ लिख सकते हैं। तो यहाँ a = 10, b = 1 लीजिए

Find the cube of 11 ( 11³= ? )

Use simple algebra formula (a + b)³ = a³ + 3a²b + 3ab² + b³.

We can write 11³ = (10 + 1 )³. So here take a = 10, b = 1

(10 + 1)³

 = 10³ + 3×10²× 1 + 3×10×1² + 1³

 = 1000 + 300 + 30 + 1 

= 1331.

28 का घन ज्ञात कीजिए ( 48³= ? )

सरल बीजगणित सूत्र (a – b)³ = a³ – 3a²b + 3ab² – b³ का उपयोग करें। 

हम 28³ = (30–2 )³ लिख सकते हैं। तो यहाँ a = 30, b = 2 लीजिए

Find the cube of 28 ( 28³= ? )

Use simple algebra formula (a + b)³ = a³ + 3a²b + 3ab² + b³.

We can write 28³ = (30 + 2 )³. So here take a = 30, b = 2

(30 – 2)³ 

 = 30³ – 3×30²× 2 + 3×30×2² – 2³

= 27000 – 5400 + 360 – 8 

= 21600 +352

= 21952.

विधि : 2 

उदाहरण 1 : 68 का घन ज्ञात कीजिये ( 68³= ? )

सूत्र लें (a + b)³ = a³ / 3a²b / 3ab² / b³। और यहाँ मान लीजिए, a = 6 और b = 8।

Method : 2

Ex. 1 : Find the cube of 68 ( 68³= ? )

Take the formula (a + b)³ = a³ / 3a²b / 3ab² / b³. And here let, a = 6 and b = 8.

68

= (6 + 8)³

= 6³ / 3×6²× 8 / 3×6×8² / 8³

 = 216 / 984 / 1152 / 512 

 = 216 / ⁹⁸4 / ¹¹⁵2 / ⁵¹2 

= 314432

चरण 1 : b³ = 8 x 8 x 8 = 512 लें। खोए हुए अंक को उत्तर के अंतिम स्थान पर लें और शेष मान को अगले चरण में जोड़ें।

अर्थात् उत्तर : _ _ _ _ _ 2 और 51 को अगले चरण में जोड़ा जाएगा।

चरण 2 : 3ab² = 3 x 6 x 64 = 3 x 384 = 1152 और 51 (पिछले चरण से) लें। तो 1152 + 51 = 1203। यहां उत्तर में खोए हुए अंक को अगले स्थान पर लें और शेष मान को अगले चरण में जोड़ें।

अर्थात उत्तर : _ _ _ _ 3 2 और 120 को अगले चरण में जोड़ना है।

चरण 3 : 3a²b =(3 x 36 x 8) + 120= 864 + 120 = 984 लें। यहां उत्तर में खोए हुए अंक को अगले स्थान पर लें और शेष मान को अगले चरण में जोड़ें।

अर्थात उत्तर : _ _ _43 2 और 98 को अगले चरण में जोड़ना है।

चरण 4: a² =(6 x 6 x 6) + 98= 216 + 98 = 314 लीजिए। इस मान को उत्तर में अगले स्थानों पर लीजिए।

यानी  उत्तर : 31443 2.

इसलिए, (68)³ = 314432.

Step 1 : Take b³ = 8 x 8 x 8 = 512. Take the lost digit to the last place of the answer and add the remaining value in the next step.

That is, Answer : _ _ _ _ _ 2 and 51 are to be added in the next step.

Step 2 : 3ab² = 3 x 6 x 64 = 3 x 384 = 1152 and take 51 (from previous step). So 1152 + 51 = 1203. Here take the lost digit to the next place in the answer and add the remaining value in the next step.

That is, Answer : _ _ _ _ 3 2 and 120 are to be added in the next step.

Step 3 : Take 3a²b =(3 x 36 x 8) + 120= 864 + 120 = 984. Here take the missing digit to the next place in the answer and add the remaining value in the next step.

i.e. Answer: _ _ _43 2 and 98 are to be added in the next step.

Step 4: Take a² =(6 x 6 x 6) + 98= 216 + 98 = 314. Take this value to the next places in the answer.

i.e. Answer: 31443 2.

So, (68)³ = 314432.

किसी भी संख्या का घन

728 का घन ज्ञात कीजिए ।

 728³= ? 

चरण 1 : संख्या को इस प्रकार विभाजित करें जैसे कि 7 / 28 या 72 / 8।

यहां हम 72 / 8 लेते हैं ।

चरण 2: पहले भाग को दूसरे भाग से विभाजित करें। यानी 72÷8 = 9. 

यहां हम a = 8, b= 9, c = 8³ = 512

चरण 3: पहले भाग का घन c = 8 x 8 x 8 = 512. 

यहां उत्तर में अंतिम अंक लें और शेष मान 51 अगले चरण में जोड़ें।

यानी उत्तर : _ _ _ _ 2 और 51 को अगले चरण में जोड़ा जाना है।

चरण 4: 3 बीसी + 51

= (3 x 9 x 512) +51

= 13824 + 51 

= 13875

यहां उत्तर में खोए हुए अंक को अगले अंक में लें और शेष मान 1387 को अगले चरण में जोड़ें।

अर्थात उत्तर : _ _ _ 5 2 और 1387 को अगले चरण में जोड़ना है।

चरण 5: 

3 बी² सी +13875

= (3 x 9 x 9 x 512) +1387

= 124416 + 1387 

= 125803। 

यहां उत्तर में खोए हुए अंक को अगले अंक में लें और शेष मान 12580 को अगले चरण में जोड़ें।

अर्थात उत्तर : _ _ _3 5 2 और 12580 को अगले चरण में जोड़ना है।

चरण 6: 

b ³ c +12580

= (9 x 9 x 9 x512) +12580

= 373248 + 12580 

= 385828

 यहां इस मान को उत्तर में लें

यानी उत्तर : 385828352।

Cube of any number

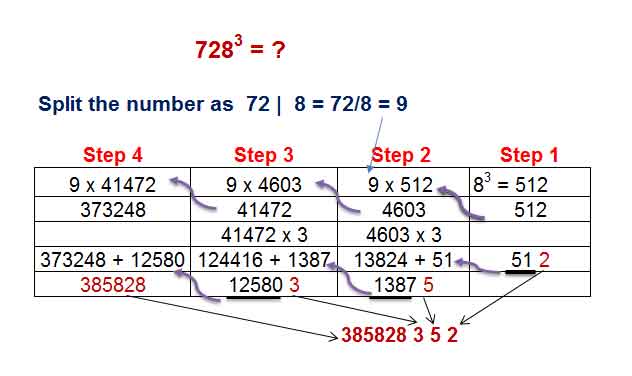
Find the cube of 728.

728³= ?

Step 1: Divide the number in such a way that it becomes 7 / 28 or 72 / 8.

Here we take 72 / 8.

Step 2: Divide the first part by the second part. i.e. 72÷8 = 9.

Here we take a = 8, b= 9, c = 8³ = 512

Step 3: Cube of first part c = 8 x 8 x 8 = 512.

Here take the last digit in the answer and add the remaining value 51 in the next step.

i.e. Answer: _ _ _ _ 2 and 51 are to be added in the next step.

Step 4: 3bc + 51

= (3 x 9 x 512) +51

= 13824 + 51

= 13875

Here take the missing digit in the answer to the next digit and add the remaining value 1387 in the next step.

That is, Answer: _ _ _ 5 2 and 1387 is to be added in the next step.

Step 5:

3b²c +13875

= (3 x 9 x 9 x 512) +1387

= 124416 + 1387

= 125803.

Here take the missing digit in the answer to the next digit and add the remaining value 12580 in the next step.

That is, Answer: _ _ _3 5 2 and 12580 is to be added in the next step.

Step 6:

b ³ c +12580

= (9 x 9 x 9 x512) +12580

= 373248 + 12580

= 385828

Here take this value as answer

i.e. Answer : 385828352.

CUBES OF NUMBERS – PART2

The Anurupya Sutra is another method of approaching cubes of numbers.

1. Put down the cube of first digit in a row of 4 figures in a geometrical ratio in the exact proportion subsisting between them
2. Put down under second and third numbers, just two times the said numbers themselves
3. Add the first and second row to get the final result

 e.g 133³                                                                                                                                                                       step1 :           1      3     9     27                               step2:                     6    18                                         step3:            1      9    27   27                                 final result: 2     1     9       7 

e.g 283³                                                                                                                                                                       step1 :           8      32    128    512                      step2:                     64    256                                  step3:            8      96    384   512                                                17         6    435         2                      final result:  21 9 5 2

Note that the method above can also be used to find the fourth power of a given number with the only difference that first row will contain 5 figures (instead of 4 above) in a geometrical ratio and second row will contain 3 figures (instead of 2 above) – twice of 2nd, 3rd and 4th digit of the first row.

CUBES OF NUMBERS – 

PART2

APRIL 11, 2018 RESHMA LEAVE A COMMENT

The Anurupya Sutra is another method of approaching cubes of numbers.

Put down the cube of first digit in a row of 4 figures in a geometrical ratio in the exact proportion subsisting between them

Put down under second and third numbers, just two times the said numbers themselves

Add the first and second row to get the final result

 e.g 1333 step1 : 1 3 9 27 step2: 6 18 step3: 1 9 27 27 final result: 2 1 9 7 

e.g 2833 step1 : 8 32 128 512 step2: 64 256 step3: 8 96 384 512 17 6 435 2 final result: 21 9 5 2

Note that the method above can also be used to find the fourth power of a given number with the only difference that first row will contain 5 figures (instead of 4 above) in a geometrical ratio and second row will contain 3 figures (instead of 2 above) – twice of 2nd, 3rd and 4th digit of the first row.

वैदिक गणित घन Cube करने का बहुत ही आसान सूत्र ज़रूर सीखें ये नई ट्रिक

वैदिक गणित  घन Cube करना होगा बहुत ही सरल | सीखें यह सरल सूत्र

वैदिक गणित घन Cube के इस सूत्र द्वारा किसी भी संख्या का घन Cube करने के लिए हमे कैलकुलेटर प्रयोग करने की आवश्यकता नही है बस इस सरल से सूत्र को समझने की ज़रूरत है तो वैदिक गणित घन Cube सूत्र सीखकर हम किसी भी 2 अंकों की संख्या का घन Cube बड़ी आसानी से निकाल सकते हैं | तो इस उदाहरण से जानिए कैसे काम करता है वैदिक गणित घन Cube का ये मैजिकल फार्मूला -:

उदहारण : 63 का घन करें |

हल : 63³ यानि 63×63×63 =?

सबसे पहले संख्या के पहले अंक का घन करें | जैसे यहाँ 6 का घन 216 है (6³= 216) अब प्रश्न संख्या के दोनों अंकों का अनुपात निकालें जिस प्रकार यहाँ 6:3 = 2: 1 है | अब प्राप्त संख्या 216 के आगे एक सीधी लाइन में 3 ओर संख्याएँ 2:1 के अनुपात: में लिखें जैसे 2:1 = 216:108 व 2:1 = 108:54 व 2:1 = 54:27

इस प्रकार हमे 4 संख्याएँ प्राप्त होती हैं 216, 108, 54 और 27 और बीच की 2 संख्याओ 108 व 54 का दोगुना उन्ही के नीचे लिखें और इनको इस प्रकार लिखें जैसे कि नीचे लिखी गयी हैं |

प्रथम चरण :

    216    108     54      27

            + 216   +108               

216      324     162      27

            250047

इस प्रकार हमे चार संख्याएँ प्राप्त होती हैं 216, 324, 162 व 27

 

इनको पीछे से हल करना शुरू करें यानि 27 से तो सही उत्तर निकाल आएगा |

अंतिम अंक 27 का 7 व 2 हासिल = _ / _ / _ / 7

162 +2 (हासिल) = 164 का 4 व 16 हासिल = _ / _ / 4 / 7

324+16 (हासिल) = 340 की 0 व 34 हासिल = _ / 0 / 4 / 7

216+34(हासिल) = 250 का 250 = 250 / 0 / 4 / 7

अतः 63³ = 250047 उत्तर