वैदिक बीजगणित (9) | बीजगणितीय गुणा |
उधर्वत्रियकम् सूत्र द्वारा
(भाग 6)
चरण 1
Formula (सूत्र)
Use SNA Formula For Multiplication
Mean
* First of all multiply Sign to Sign and
* Then Number to Number and
* Then same Alphabet (Variables) to same Alphabet (Variables) and add the power of same variables.
उधर्वत्रियकम् सूत्र द्वारा
2T × 2T
I X I
[आई एक्स आई ]
A + B
C + D
A×C / A×D + C×B / B×D
1. Multiply the binomials to binomial and Find the product.
निम्न द्विपदों की द्विपदों से गुणा करों तथा गुणनफल ज्ञात करो।
01. (5 – 2x) (3 + x)
02. (x + 7y) (7x – y)
03. (a² + b) (a + b² )
04. (p² – q² ) (2p + q)
05. (a + b)(a + b)
06. (x + 3) (x + 3)
07. (2y + 5) (2y + 5)
08. (2a – 7) (2a – 7)
09. (2a – 3b) (2a – 4b)
10. (2a – 5b) (2a – 7b)
11. (a² + b² ) (– a² + b² )
12. (6x – 7) (6x + 7)
13. (– a + c) (– a + c)
14. (x + 3) (x + 7)
15. (4x + 5) (4x + 1)
16. (4x – 5) (4x – 1)
17. (4x + 5) (4x – 1)
18. (2x + 5y) (2x + 3y)
19. (2a² + 9) (2a² + 5)
20. (xyz – 4) (xyz – 2)
Sol. 01.
(5 – 2x) (3 + x)
Or
5 – 2x
3 + x
5 ×3 / 5×x – 3 × 2x / –2x × x
15 / 5x – 6x / –2x²
= 15 – 1x – 2x² Ans.
उधर्वत्रियकम् सूत्र द्वारा
3T × 3T
I x X x I
[आई एक्स बिगएक्स एक्स आई ]
(A + B + C)(D + E + F)
A + B + C
D + E + F
A×D/AE+BD/AF+DC+BE/EC+BF/FC
(Write in Standard form)
2. Multiply the binomials by trinomial or polynomials and Find the product.
निम्न द्विपदों व त्रिपदों या बहुपदों से गुणा करों तथा गुणनफल ज्ञात करो।
01. (3 + x + y)(3 + x + y)
02. (7x – y + 3) (7x – y + 3)
03. (a + 2 + b) (a + b – 5)
04. (p² – q² +5) (2p + q + 7)
05. (a + b + 2)(a + b + 8)
06. (x + y + 3) (x² + x + 3)
07. (3y² + 2y + 5) (2y² + y + 5)
08. (2a – 3b +2) (2a – 4b + 6)
09. (2a – 5b – 4) (2a – 7b + 1)
10. (4 + a² + b² ) (5– a² + b² )
11. (x² + 6x – 7) (6x² + x + 7)
12. (3– a + c) (8 – a + c)
13. (x² + x + 3) (x² + x + 7)
14. (x² +4x + 5) (4x² +x + 1)
15. (a² +2a – 7) (2a² + a – 7)
Sol. 01. (3 + x + y)(3 + x + y)
3 + x + y
3 + x + y
3×3/3x+3x/3y+3y+x²/xy+xy/y²
9/+6x/+6y+x²/+2xy/+y²
x² + y² + 6x + 6y + 2xy
(Write in Standard form)
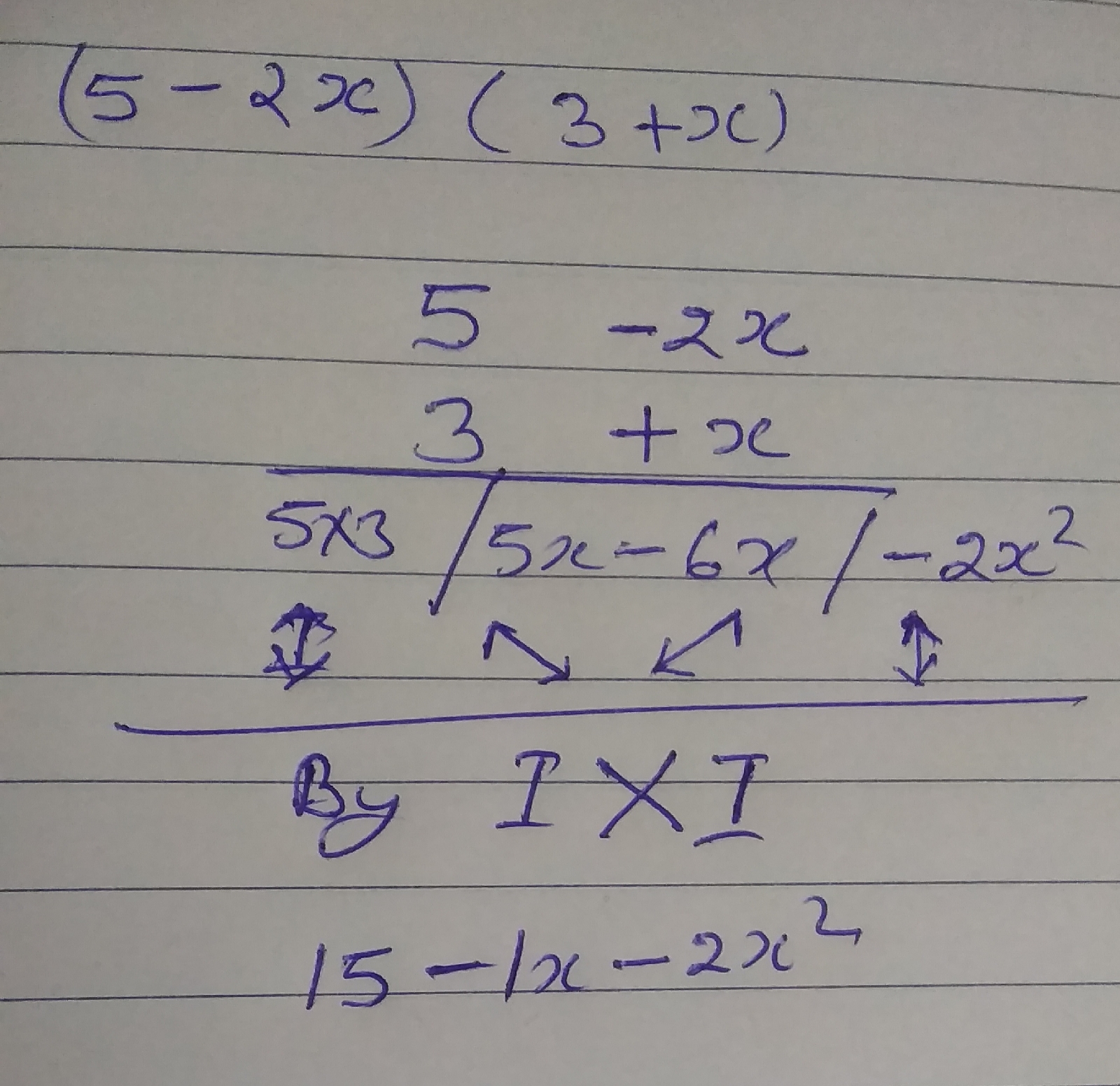
Post a Comment
Post a Comment