Square
वर्ग संक्रिया
These are the methods of squaring in Vedic mathematics.
- Ekadhikena Purvena
- Anurupyena
- Nikhilam or Yavadunam Tavadunikrtya Varganca Yojayet
- Urdhva – tiryagbhyam
- Sankalana - Vyavakalanabhyam
1. Ekadhikena Purvena (एकाधिकेन पूर्वेण):
Ekadhikena Purvena means “By one more than the previous one”
‘पहले से एक अधिक के द्वारा’
The Sutra signifies number of which the last digit is 5. That means the Sutra works in squaring of numbers like, 15, 25, 35, 95 or 205. Multiplication of the last digits gives the right hand part of the answer.
जिन अंकों के चरमं (अन्तिम) अंक 5 हो तथा शेष निखिलम् अंक समान हो, का वर्ग इस विधि द्वारा किया जाता हैं। (जैसे-15, 25, 35, 95 or 205), यहाँ प्रत्येक प्रश्न में चरमं अंक का वर्ग उत्तर का दायाँ भाग होता हैं।
सूत्र आधारित विधि:
1. वर्ग के दो पक्ष होते हैं- दाहिना तथा बायाँ।
2. चरमं अंक का वर्ग दायीं ओर लिखते हैं।
3. बायें पक्ष में शेष निखिलम् अंक तथा शेष निखिलम् अंक के एकाधिक का गुणनफल लिखते हैं।
Example: 35 X 35
35 X 35
= 3 x 4 / 5 x 5
= 12 /25
= 1225
1. square of the last digits (RHS) 5X5 =25, RHS=25
2. LHS 3 x (3+1) =12
Example: 85 X 85
85 X 85
= 8 x 9 / 5 x 5
= 72 /25 = 7225
1. चरमं अंक का वर्ग (दाहिना पक्ष), 5X5 =25,
2. बायाँ पक्ष, 8 x (8+1) =72
Example: 4.5 X 4.5
4.5 x 4.5
= 4 x 5 / 0.5 x 0.5
= 20 /0.25 = 20.25
1. square of the last digits (RHS) 0.5X0.5 =0.25,
2. LHS 4 x (4+1) =20
2. Anurupyena (उपसूत्र - आनुरूप्येण):
The upa-Sutra 'Anurupyena' means 'proportionality' or 'similarly'.
‘अनुपातों से’
इस सूत्र के उपयोग से दो अंकों की संख्या का वर्ग ज्ञात किया जाता हैं।
This Sutra is highly useful to find square of two numbers.
सूत्र आधारित विधि:
1. वर्ग के उत्तर के लिए तीन खण्ड़ बनाते हैं।
2. प्रथम खण्ड़ में दहाई अंक का वर्ग तथा तीसरे खण्ड़ में इकाई अंक का वर्ग लिखते हैं।
3. मध्य खण्ड़ में दोनो अंकों का गुणनफल लिखते हैं।
4. मध्य खण्ड़ में दोनो अंकों का गुणनफल नीचे एक बार और लिखते हैं।
5. योगफल संख्या का अभीष्ट वर्ग होता हैं। योग करते समय मध्य तथा तीसरे खण्ड़ में एक अंक ही लिखते हैं। दो अंक होने पर अंकों को समायोजित करते हैं।
Example: 472 =47 X 47
| संकेत 1. प्रथम खण्ड़ में दहाई अंक का वर्ग = 42 = 16 2. तीसरे खण्ड़ में इकाई अंक का वर्ग = 72= 49 3. मध्य खण्ड़ में दोनो अंकों का गुणनफल = 4X7=28 4. मध्य खण्ड़ में दोनो अंकों का गुणनफल नीचे एक बार और लिखते हैं। 5. योगफल संख्या का अभीष्ट वर्ग होता हैं। 6. अभीष्ट वर्ग = 2209
|
Example: 972 =97 X 97
| संकेत 1. प्रथम खण्ड़ में दहाई अंक का वर्ग = 92 = 81 2. तीसरे खण्ड़ में इकाई अंक का वर्ग = 72= 49 3. मध्य खण्ड़ में दोनो अंकों का गुणनफल = 9X7=63 4. मध्य खण्ड़ में दोनो अंकों का गुणनफल नीचे एक बार और लिखते हैं। 5. योगफल संख्या का अभीष्ट वर्ग होता हैं। 6. अभीष्ट वर्ग = 9407
|
3. Sutra Nikhilam (निखिलम् सूत्र – आधार-उपाधार) या यावदूनम् तावदूनम् कृत्य वर्ग च योजयेत्:
Ø Nikhilam निखिलम् सूत्र आधार प्रयोग -
जब संख्या आधार 10 , 100 या 10 की घात के निकट हो तो उसका वर्ग, सूत्र निखिलम्-आधार द्वारा ज्ञात किया जाता हैं।
सूत्र आधारित विधि:
1. संख्या का निकटतम आधार चुनकर विचलन ज्ञात करते हैं।
विचलन = संख्या - आधार
2. आधार के सापेक्ष विचलन को संख्या के सामने लिखते हैं।
3. तिरछी रेखा से वर्ग स्थान के दो भाग करते हैं।
4. दायें पक्ष में विचलन का वर्ग लिखते हैं।
5. बायें पक्ष में संख्या तथा विचलन का योग लिखते हैं।
6. आधार में जितने शून्य हो, उतने ही अंक दायें पक्ष में रखते हैं।
· यदि आधार 10 हो तो दायें पक्ष में एक अंक रहेगा, दो अंक हो तो दहाई का अंक बायें पक्ष में जोड़ देते हैं।
· यदि आधार 100 हो तो दायें पक्ष में दो अंक रहेंगे, एक अंक हो तो उससे पूर्व 0 लिखते हैं, तीन अंक हो तो सैंकडे़ का अंक बायें पक्ष में जोड़ देते हैं।
Example: 122 =12 X 12
| संकेत 1. निकटतम आधार 10 अत: विचलन विचलन = 12 – 10 = +2 2. संख्या के सामने विचलन लिखते हैं। 3. तिरछी रेखा से उत्तर वाले भाग के दो भाग करते हैं। 4. उत्तर के दायें पक्ष में विचलन का वर्ग 22 = 4 लिखते हैं। 5. बायें पक्ष में संख्या तथा विचलन का योग 12+(+2) = 14 लिखते हैं। 6. अभीष्ट वर्ग = 144
|
Example: 922 = 92 X 92
| संकेत 1. निकटतम आधार 100 अत: विचलन विचलन = 92 – 100 = - 08 2. संख्या के सामने विचलन लिखते हैं। 3. तिरछी रेखा से उत्तर वाले भाग के दो भाग करते हैं। 4. उत्तर के दायें पक्ष में विचलन का वर्ग (-08)2 = 64 लिखते हैं। 5. बायें पक्ष में संख्या तथा विचलन का योग 192+(-08) = 84 लिखते हैं। 6. अभीष्ट वर्ग = 8464
|
Ø Nikhilam निखिलम् सूत्र आधार प्रयोग -
जब संख्या आधार 10 , 100 या 10 की घात के निकट नही हो तो उसका वर्ग, सूत्र निखिलम्-उपाधार द्वारा ज्ञात किया जाता हैं।
सूत्र आधारित विधि:
1. संख्या का निकटतम उपाधार चुनकर विचलन ज्ञात करते हैं।
विचलन = संख्या - उपाधार
2. उपाधार के सापेक्ष विचलन को संख्या के सामने लिखते हैं।
3. तिरछी रेखा से वर्ग स्थान के दो भाग करते हैं।
4. दायें पक्ष में विचलन का वर्ग लिखते हैं।
5. बायें पक्ष में संख्या तथा विचलन के योग को उपाधार से गुणा कर लिखते हैं।
6. आधार में जितने शून्य हो, उतने ही अंक दायें पक्ष में रखते हैं।
· यदि आधार 10 हो तो दायें पक्ष में एक अंक रहेगा, दो अंक हो तो दहाई का अंक बायें पक्ष में जोड़ देते हैं।
· यदि आधार 100 हो तो दायें पक्ष में दो अंक रहेंगे, एक अंक हो तो उससे पूर्व 0 लिखते हैं, तीन अंक हो तो सैंकडे़ का अंक बायें पक्ष में जोड़ देते हैं।
Example: 322 = 32 X 32
| संकेत 1. निकटतम आधार 10 तथा उपाधार = 10 x 3 = 30 अत: विचलन = 32 – 30 = +2 2. संख्या के सामने विचलन लिखते हैं। 3. तिरछी रेखा से उत्तर वाले भाग के दो भाग करते हैं। 4. उत्तर के दायें पक्ष में विचलन का वर्ग 22 = 4 लिखते हैं। 5. बायें पक्ष में संख्या तथा विचलन का योग 32+(+2) = 34 लिखते हैं। 6. समायोजन करने पर बायाँ पक्ष = 34 x 3 = 102 एवं दायाँ पक्ष = 4 7. अभीष्ट वर्ग = 1024 |
Example: 572 = 57 X 57
| संकेत 1. निकटतम आधार 10 तथा उपाधार = 10 x 5 = 50 अत: विचलन = 57 – 50 = +7 2. संख्या के सामने विचलन लिखते हैं। 3. तिरछी रेखा से उत्तर वाले भाग के दो भाग करते हैं। 4. उत्तर के दायें पक्ष में विचलन का वर्ग 72 = 49 लिखते हैं। 5. बायें पक्ष में संख्या तथा विचलन का योग 57+(+7) = 64 लिखते हैं। 6. समायोजन करने पर बायाँ पक्ष = 64 x 5 = 320 एवं दायाँ पक्ष = 49 7. दायें पक्ष में एक अंक होना चाहिये अत: 4 को बायें पक्ष में जोड़ते हैं। 8. बायाँ पक्ष = 320+4 = 324 एवं दायाँ पक्ष = 9 9. अभीष्ट वर्ग = 3249 |
4. Urdhva tiryak sutra (ऊर्ध्व तिर्यक सूत्र) आधारित द्वन्द्व योग विधि -
सूत्र ऊर्ध्व तिर्यक आधारित द्वन्द्व योग विधि द्वारा किसी भी संख्या का वर्ग ज्ञात किया जा सकता हैं। यह क्रिया बायें तथा दायें दोनो तरफ से प्रारम्भ की जा सकती हैं।
सूत्र पर आधारित विधि:
1. सर्व प्रथम संख्या का समूह बनाते हैं।
अंक समूह संख्या = (संख्या में अंकों की संख्या X 2) – 1
· दो अंकों की संख्या के तीन अंक समूह होंगे। जैसे- 12 के अंक समूह =1, 12 व 2
· तीन अंकों की संख्या के पांच अंक समूह होंगे। जैसे- 123 के अंक समूह =1, 12, 123, 23 व 3
2. अंक समूह के द्वन्द्व योग ज्ञात करते हैं।
· एक अंक की संख्या का द्वन्द्व योग = उस अंक का वर्गZ
· दो अंकों की संख्या का द्वन्द्व योग = दोनो अंकों के गुणनफल का दुगना
· तीन अंकों की संख्या का द्वन्द्व योग = पहले व तीसरे अंक का गुणनफल X 2 + मध्य अंक का वर्ग
· चार अंकों की संख्या का द्वन्द्व योग = पहले व चौथे अंक का गुणनफल X 2 + दूसरे व तीसरे अंक का गुणनफल X 2
Number | Dwandwa yog (Duplex) |
3 | 32 = 9 |
6 | 62 = 36 |
34 | (3X4)2 = 24 |
56 | (5X6)2 = 60 |
105 | (1X5)2+02= 10+0 = 10 |
345 | (3X5)2+42=30+16 = 46 |
1435 | (1X5)2+(4X3)2=10+24 = 34 |
3. अंक समूह के द्वन्द्व योग ज्ञात कर उन्हें उसी क्रम में रखते हैं।
4. इकाई अंक की ओर से योग करते हैं, तथा एक खण्ड़ में एक अंक लिखते हैं। योगफल ही संख्या का अभीष्ट वर्ग होता हैं।
Example: 322 = 32 X 32
32 के अंक समूह = 3, 32 व 2
322 = 3 का द्वन्द्व योग / 32 का द्वन्द्व योग / 2 का द्वन्द्व योग
= 32 / (3X2) X2 / 22
= 9 / 12 / 4
= 9 / 12 / 4
= 1024
Example: 3422 = 342 X 342
342 के अंक समूह = 3, 34, 342, 42 व 2
3422 = 32 / (3X4) X2 / (3X2) X2 + 42/ (4X2) X2 / 22
= 9 / 24 / 12+16 / 16 / 4
= 9 / 24 / 28 /16 / 4
= 9 / 24 / 28 / 16 / 4
= 116964
Example: 12342 =1234X 1234
1234 के अंक समूह = 1, 12,123, 1234, 234, 34 व 4 12342 = 12 / (1X2) X2 / (1X3) X2 + 22/ (1X4) X2 + (2X3) X2 / (2X4) x2+32 / (3X4) X2 / 42 = 1 / 4/ 6+4 / 8+12 / 16+9 / 24 / 16 = 1 / 4 / 10 /20 / 25 / 24 / 16 = 1 / 4 / 10 / 20 / 25 / 24 / 16 = 1522756 |
Example: 272 =27X 27
27 के अंक समूह = 2, 27 व 7
272 = 22 / (2X7) X2 / 72
= 4 / 28/ 49
= 4 / 28 / 49
= 729
5. Sankalana - Vyavakalanabhyam (संकलन - व्यवकलनाभ्याम्) आधारित इष्ट संख्या विधि –
Ø भास्कराचार्य द्वितीय रचित 'लीलावती' में वर्ग ज्ञात करने की संकलन-व्यवकलन आधारित इष्ट संख्या विधि का वर्णन मिलता हैं। इस विधि के अनुसार यदि कोई संख्या X तथा इष्ट संख्या a हो तो x2 = (x + a) (x - a)+a2; सूत्र द्वारा किसी भी संख्या का वर्ग ज्ञात किया जा सकता हैं। जब संख्या में इष्ट संख्या जोड़ने या घटाने पर एक शून्यान्त संख्या प्राप्त होती हैं, तब यह विधि अधिक प्रभावी होती हैं, तथा उपसूत्र यावदूनम् तावदूंनम् कृत्य वर्ग च योजयेत् का रूप ले लेती हैं।
Example: 322 = 32 X 32 इष्ट संख्या = 2
322 = (32+2) (32-2) +22
= 34 X 30 + 4
= 1020 + 4
= 1024
Example: 892 = 89 X 89 इष्ट संख्या = 1
892 = (89+1) (89-1) +12
= 90 X 88 + 1
= 7920 + 1
= 7921
Example: 1082 = 108 X 108 इष्ट संख्या = 8
1082 = (108+8) (108-8) +82
= 116 X 100 + 64
= 11600 + 64
= 11664
Example: 2972 = 297 X 297 इष्ट संख्या = 3
2972 = (297+3) (297-3) +32
= 300 X 294 + 9
= 88200 + 9
= 88209

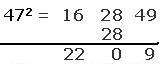

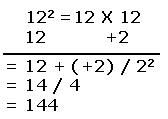
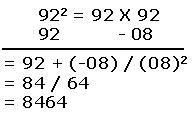
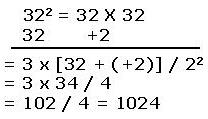
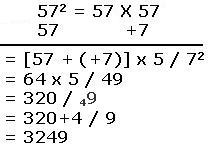
Post a Comment
Post a Comment